If any part of this notebook is used in your research, please cite with the reference found in README.md.
Demostrating network-based optimal facility location modeling
Integrating pysal/spaghetti with Cbc and ortools
Author: James D. Gaboardi jgaboardi@gmail.com
This notebook provides a use case for:
- Introducing four fundamental optimal facility location models
- Utilizing the data structures provided by
spaghettias input for optimization problems - Solving the models, and comparing and visualizing the results
%load_ext watermark
%watermark
In addtion to the base spaghetti requirements (and their dependecies), this notebook requires installations of:
- descartes
$ conda install -c conda-forge descartes
- geopandas
$ conda install -c conda-forge geopandas
- matplotlib
$ conda install matplotlib
- ortools
$ pip install ortools
- seaborn
$ conda install seaborn
import spaghetti
import sys, warnings
from collections import OrderedDict
import geopandas
import libpysal
from libpysal import cg, examples
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import matplotlib.patches as mpatches
from matplotlib.colors import ListedColormap
import numpy
import ortools
from ortools.linear_solver import pywraplp
import seaborn
import shapely
from shapely.geometry import Point
try:
from IPython.display import Markdown as md
from IPython.display import set_matplotlib_formats
set_matplotlib_formats("retina")
except ImportError:
pass
%matplotlib inline
%watermark -w
%watermark -iv
1.1 Scenario:
The Neighborhood X Planning Committee has been asked by residents to set up a Little Free Library program to supplement the community's growing reading needs, as 15 families just moved in bring the total household count to 400. Since the neighborhood can't afford to have a library on every corner, the committee must decide on where to locate them and how to do so in a transparent manner. There are currently 14 candidate sites in the neighborhood for Little Free Libraries and the community can afford to support up to 5 locations, but would preferably support 3 locations with the extra budget going towards new books and unforseen maintenance costs. The committee also must locate all the libraries within 1 km of all households, but preferably with .8km. As it turns out one of the committee members is an Operations Research professor at the local university, Dr. Minimax, and volunteers to build 4 models to optimally site the Little Free Libraries acording to objective functions and specific sets of contraints. She puts forth 4 facility location models:
Location Set Covering Problem
- Site the minimum number of facilities to cover all demand (clients) within a specified service radius.
- Originally Published:
Toregas, C. and ReVelle, Charles. 1972. Optimal Location Under Time or Distance Constraints. Papers of the Regional Science Association. 28(1):133 - 144.
p-median Problem
- Site a predetermined number of facilities while minimizing total weighted distance.
- Originally Published:
S. L. Hakimi. 1964. Optimum Locations of Switching Centers and the Absolute Centers and Medians of a Graph. Operations Research. 12 (3):450-459.
p-center Problem
- Site a predetermined number of facilities while minimizing the worst-case travel distance.
- Originally Published:
S. L. Hakimi. 1964. Optimum Locations of Switching Centers and the Absolute Centers and Medians of a Graph. Operations Research. 12 (3):450-459.
Maximal Covering Location Problem
- Site a predetermined number of facilities while maximizing demand coverage within a specified service radius.
- Originally Published:
Church, R. L and C. ReVelle. 1974. The Maximal Covering Location Problem. Papers of the Regional Science Association. 32:101-18.
# n clients and n facilities
client_count, facility_count = 400, 14
# candidate facilites to site
p_facilities = 3
# maximum coverage meters
max_coverage = 1000.0
# minimum coverage meters
min_coverage = 800.0
random_seeds = {"client": 3006, "facility": 1520}
title = "Neighborhood X"
class FacilityLocationModel:
"""Solve a facility location optimization model
Parameters
----------
name : str
Problem model name; must also be defined as a class method.
cij : numpy.ndarray
cost matrix from origins (index of i) to destination (index of j).
Default is None.
ai : numpy.ndarray
Client weight vector. Default is None.
s : float
service radius. Default is None.
p : int
Density of facilities to site. Default is None.
write_lp : str
file name (and path) of the LP file to write out.
print_sol : bool
print select results. Default is True.
Methods
-------
build_lscp : build location set covering problem
build_pmp : build p-median problem
build_pcp : build p-center problem
build_mclp : build maximal covering location problem
add_vars : add variables to a model
add_constrs : add contraints to a model
add_obj : add an objective function to a model
optimize : solve a model
record_decisions : record optimal decision variables
non_obj_vals : record non-objective values stats (eg. percent covered)
print_results : print selected results
Attributes
----------
model : ortools.linear_solver.pywraplp.Solver
proxy of <Swig Object of type 'operations_research::MPSolver *'
n_cli : int
total client sites
r_cli : range
iterable of client sites
n_fac : int
total candidate facility sites
r_fac : range
iterable of candidate facility sites
aij : numpy.ndarray
binary coverage matrix from cij (within s service radius)
sij : numpy.ndarray
demand weighted cost matrix as (ai * cij).
fac_vars : dict
facility decision variables
cli_vars : dict
client decision variables
W : ortools.linear_solver.pywraplp.Variable
minimized maximum variable in the p-center problem formulation
lp_formulation : str
linear programming formulation of the model
solve_minutes : float
solve time in minutes
obj_val : int or float
model objective value
fac2cli : dict
facility to client relationship lookup
cli2fac : dict
client to facility relationship lookup
fac2iloc : dict
facility to dataframe index location lookup
n_cli_uncov : int
count of client location outside the service radius
cli2ncov : dict
client to covered by count lookup
ncov2ncli : dict
covered by count to client count lookup
mean_dist :
mean distance per person to the assigned facility
perc_served :
percentage of weighted clients covered in `s`
"""
def __init__(
self, name, ai=None, cij=None, s=None, p=None, write_lp=None, print_sol=True
):
# Set model information
self.name = name
# create a solver instance
solver_instance = pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING
# instantiate a model
self.model = pywraplp.Solver(self.name, solver_instance)
# Set parameters and indices
# facility parameter
if p:
self.p = p
# client count and range
self.cij = cij
self.n_cli = cij.shape[0]
self.r_cli = range(self.n_cli)
# facility count and range
self.n_fac = self.cij.shape[1]
self.r_fac = range(self.n_fac)
# demand parameter
if ai is not None:
self.ai = ai
self.ai_sum = ai.sum()
# weighted demand
try:
self.sij = self.ai * self.cij
except ValueError:
self.ai = self.ai.values.reshape(self.n_cli, 1)
self.sij = self.ai * self.cij
# if the model has a service radius parameter
if s:
self.s = s
# binary coverage matrix from cij
self.aij = numpy.zeros(self.cij.shape)
self.aij[self.cij <= self.s] = 1.0
# Set decision variables, constraints, and objective function
try:
getattr(self, "build_" + self.name)()
except:
raise AttributeError(self.name, "not a defined location model.")
# solve
self.optimize(write_lp=write_lp)
# records seleted decision variables
self.record_decisions()
# record non-objective values stats (eg. percent covered)
self.non_obj_vals()
# print results
if print_sol:
self.print_results()
def build_lscp(self):
""" Integer programming formulation of the Location Set Covering Problem.
Originally Published:
Toregas, C. and ReVelle, Charles. 1972.
Optimal Location Under Time or Distance Constraints.
Papers of the Regional Science Association. 28(1):133 - 144.
"""
# Decision Variables
self.add_vars()
# Constraints
self.add_constrs(constr=1) # set coverage constraints
# Objective Function
self.add_obj()
def build_pmp(self):
"""Integer programming formulation of the p-median Problem.
Originally Published:
S. L. Hakimi. 1964. Optimum Locations of Switching Centers and
the Absolute Centers and Medians of a Graph. Operations Research.
12 (3):450-459.
Adapted from:
-1-
ReVelle, C.S. and Swain, R.W. 1970. Central facilities location.
Geographical Analysis. 2(1), 30-42.
-2-
Toregas, C., Swain, R., ReVelle, C., Bergman, L. 1971. The Location
of Emergency Service Facilities. Operations Research. 19 (6),
1363-1373.
- 3 -
Daskin, M. (1995). Network and discrete location: Models, algorithms,
and applications. New York: John Wiley and Sons, Inc.
"""
# Decision Variables
self.add_vars()
# Constraints
self.add_constrs(constr=2) # assignment constraints
self.add_constrs(constr=3) # facility constraint
self.add_constrs(constr=4) # opening constraints
# Objective Function
self.add_obj()
def build_pcp(self):
"""Integer programming formulation of the p-center Problem.
Originally Published:
S. L. Hakimi. 1964. Optimum Locations of Switching Centers and
the Absolute Centers and Medians of a Graph. Operations Research.
12 (3):450-459.
Adapted from:
Daskin, M. (1995). Network and discrete location: Models, algorithms,
and applications. New York: John Wiley and Sons, Inc.
"""
# Decision Variables
self.add_vars()
# Constraints
self.add_constrs(constr=2) # assignment constraints
self.add_constrs(constr=3) # facility constraint
self.add_constrs(constr=4) # opening constraints
self.add_constrs(constr=5) # minimized maximum constraints
# Objective Function
self.add_obj()
def build_mclp(self):
"""Integer programming formulation of the Maximal Covering Location Problem.
Originally Published:
Church, R. L and C. ReVelle. 1974. The Maximal Covering Location
Problem. Papers of the Regional Science Association. 32:101-18.
"""
# Decision Variables
self.add_vars()
# Constraints
self.add_constrs(constr=3) # facility constraint
self.add_constrs(constr=6) # maximal coverage constraints
# Objective Function
self.add_obj()
def add_vars(self):
"""Add variables to a model.
"""
# facility decision variables
self.fac_vars = {j: self.model.IntVar(0, 1, "y[%i]" % (j)) for j in self.r_fac}
# client decision variables
if self.name == "mclp":
self.cli_vars = {
(i): self.model.IntVar(0, 1, "x[%i]" % (i)) for i in self.r_cli
}
if self.name == "pmp" or self.name == "pcp":
self.cli_vars = {
(i, j): self.model.IntVar(0, 1, "x[%i,%i]" % (i, j))
for i in self.r_cli
for j in self.r_fac
}
# minimized maximum variable
if self.name == "pcp":
self.W = self.model.NumVar(0, self.model.infinity(), "W")
def add_constrs(self, constr=None):
""" Add constraints to a model.
(1) set coverage constraints
y1 + x2 >= 1
x1 + x3 >= 1
x2 >= 1
(2) assignment constraints
x1_1 + x1_2 + x1_3 = 1
(3) facility constraints
y1 + y2 + y3 = p
(4) opening constraints
- x1_1 + y1 >= 0
- x2_1 + y1 >= 0
- x3_1 + y1 >= 0
(5) minimax constraints
cost1_1*x1_1 + cost1_2*x1_2 + cost1_3*x1_3 - W <= 0
(6) maximal coverage constraints
- x1 + y1 + y3 >= 0
- x2 + y4 >= 0
Parameters
----------
constr : int {1, 2, 3, 4, 5, 6}
Contraint type to add to model. See above for explanation.
Default is None.
"""
# 1 - set covering constraints
if constr == 1:
for i in self.r_cli:
self.model.Add(
self.model.Sum(
[self.aij[i, j] * self.fac_vars[j] for j in self.r_fac]
)
>= 1
)
# 2 - assignment constraints
elif constr == 2:
for i in self.r_cli:
self.model.Add(
self.model.Sum([self.cli_vars[i, j] for j in self.r_fac]) == 1
)
# 3 - facility constraint
elif constr == 3:
self.model.Add(
self.model.Sum([self.fac_vars[j] for j in self.r_fac]) == self.p
)
# 4 - opening constraints
elif constr == 4:
for i in self.r_cli:
for j in self.r_fac:
self.model.Add(self.fac_vars[j] - self.cli_vars[i, j] >= 0)
# 5 - minimax constraints
elif constr == 5:
for i in self.r_cli:
self.model.Add(
self.model.Sum(
[self.cij[i, j] * self.cli_vars[i, j] for j in self.r_fac]
)
<= self.W
)
# 6 - max coverage constraints
elif constr == 6:
for i in self.r_cli:
self.model.Add(
self.model.Sum(
[self.aij[i, j] * self.fac_vars[j] for j in self.r_fac]
)
>= self.cli_vars[i]
)
def add_obj(self):
""" Add an objective function to a model.
"""
if self.name == "lscp":
self.model.Minimize(self.model.Sum([self.fac_vars[j] for j in self.r_fac]))
elif self.name == "pmp":
obj = [
self.sij[i, j] * self.cli_vars[i, j]
for i in self.r_cli
for j in self.r_fac
]
self.model.Minimize(self.model.Sum(obj))
elif self.name == "pcp":
self.model.Minimize(self.W)
elif self.name == "mclp":
obj = [self.ai.flatten()[i] * self.cli_vars[i] for i in self.r_cli]
self.model.Maximize(self.model.Sum(obj))
def optimize(self, write_lp=False):
""" Solve the model.
Parameters
----------
write_lp : bool
write out the linear programming formulation
"""
def _redirect_to_file(self, text):
""" Write out the model in linear programming format.
Parameters
----------
text : str
full lp formulation in str format
"""
original = sys.stdout
sys.stdout = open(self.name + ".lp", "w")
print(text)
sys.stdout = original
self.model.Solve()
# linear programming formulation
if write_lp:
self.lp_formulation = self.model.ExportModelAsLpFormat(True)
self._redirect_to_file(self.lp_formulation)
# WallTime() in milliseconds
self.solve_minutes = self.model.WallTime() * 1.66667e-5
self.obj_val = self.model.Objective().Value()
def record_decisions(self):
"""record decision variable relationship
folowing optimization.
"""
# facility-to-dataframe index location lookup
self.fac2iloc = {v.name(): k for k, v in self.fac_vars.items()}
# client-to-dataframe index location lookup
self.cli2iloc = {}
# facility-to-client lookup
self.fac2cli = {}
# record client/service relationships
for j in self.r_fac:
if self.fac_vars[j].solution_value() > 0:
jvar = self.fac_vars[j].name()
self.fac2cli[jvar] = []
for i in self.r_cli:
ivar = None
if self.name == "lscp":
if self.aij[i, j] > 0:
ivar = "x[%i]" % i
self.fac2cli[jvar].append(ivar)
elif self.name == "mclp":
if self.cli_vars[i].solution_value() > 0:
if self.aij[i, j] > 0:
ivar = self.cli_vars[i].name()
self.fac2cli[jvar].append(ivar)
else:
if self.cli_vars[i, j].solution_value() > 0:
ivar = self.cli_vars[i, j].name()
ivar = ivar.split(",")[0] + "]"
self.fac2cli[jvar].append(ivar)
if ivar:
self.cli2iloc[ivar] = i
# client-to-facility lookup
self.cli2fac = {}
for cv in list(self.cli2iloc.keys()):
self.cli2fac[cv] = []
for k, v in self.fac2cli.items():
if cv in v:
self.cli2fac[cv].append(k)
# count of uncovered clients
self.n_cli_uncov = self.n_cli - len(self.cli2iloc.keys())
# clients of clients covered by n facilities
if self.name == "lscp" or self.name == "mclp":
self.cli2ncov = {}
for c, fs in self.cli2fac.items():
self.cli2ncov[c] = len(fs)
most_coverage = max(self.cli2ncov.values())
self.ncov2ncli = {}
for cov_count in range(most_coverage + 1):
if cov_count == 0:
self.ncov2ncli[cov_count] = self.n_cli_uncov
continue
if not cov_count in list(self.cli2ncov.keys()):
self.ncov2ncli[cov_count] = 0
for c, ncov in self.cli2ncov.items():
if ncov >= cov_count:
self.ncov2ncli[cov_count] += 1
def non_obj_vals(self):
"""
"""
if self.name == "pmp":
self.mean_dist = self.obj_val / float(self.ai_sum)
if self.name == "mclp":
self.perc_served = (self.obj_val / float(self.ai_sum)) * 100.0
def print_results(self):
"""print select results
"""
print("Solve Time:", self.solve_minutes, "minutes")
# solve time and objective value
if self.name == "lscp":
u1 = "facilities needed for total coverage within a "
u2 = "%f meter service radius" % self.s
if self.name == "pmp":
u1 = "total weighted distance with "
u2 = "%i selected facilities" % self.p
if self.name == "pcp":
u1 = "worst case distance with "
u2 = "%i selected facilities" % self.p
if self.name == "mclp":
u1 = "residents within %f meters of " % self.s
u2 = "%i selected facilities" % self.p
units = u1 + u2
print("Obj. Value:", self.obj_val, units)
if self.name == "pmp":
print("Mean weighted distance per", "person: %f" % self.mean_dist)
if self.name == "mclp":
print(
"Percent of %i" % self.ai_sum, "clients covered: %f" % self.perc_served
)
# coverage values
if self.name == "lscp" or self.name == "mclp":
for ncov, ncli in self.ncov2ncli.items():
if ncov == 0:
print("--- %i clients are not covered" % ncli)
else:
if ncov == 1:
sp = "y"
else:
sp = "ies"
print(
"--- %i clients are covered" % ncli,
"by %i" % ncov,
"facilit" + sp,
)
def add_results(model, cli_df, fac_df, print_solution=False):
"""Add decision variable relationships to a dataframe.
Parameters
----------
model : ortools.linear_solver.pywraplp.Solver
proxy of <Swig Object of type 'operations_research::MPSolver *'
cli_df : geopandas.GeoDataFrame
GeoDataFrame of client locations
fac_df : geopandas.GeoDataFrame
GeoDataFrame of facility locations
print_solution : bool
print out solution decision variables. Default is False.
Returns
-------
cli_df : geopandas.GeoDataFrame
updated client locations
fac_df : geopandas.GeoDataFrame
updated facility locations
"""
col_name = model.name + "_sol"
fillers = [[cli_df, "cli2fac"], [fac_df, "fac2cli"]]
for df, attr in fillers:
df[col_name] = df["dv"].map(getattr(model, attr))
df[col_name].fillna("closed", inplace=True)
if print_solution:
selected = fac_df[fac_df[col_name] != "closed"]
for idx in selected.index:
print("")
print(selected.loc[idx, "dv"], "serving:", selected.loc[idx, col_name])
return cli_df, fac_df
def plotter(
fig=None,
base=None,
plot_aux=None,
buffered=None,
model=None,
pt1_size=None,
pt2_size=None,
plot_res=None,
save_fig=False,
title=None,
figsize=(10, 10),
):
""" Top-level scenario plotter for location analytics.
Parameters
----------
fig : matplotlib.figure.Figure
complete figure to plot. Default is None.
base : matplotlib.axes._subplots.AxesSubplot
individual axis to plot. Default is None.
plot_aux : dict
model data parameters dataframes to plot keyed by
descriptive names. Default is None.
plot_res : dict
model data results dataframes to plot keyed by
descriptive names. Default is None.
buffered : see
buffer distance from roads segments in `plot_base`.
Default is None.
pt1_size : float or float
size of points to plot. `pt1_size` should always be the
larger between `pt2_size` and `pt1_size`. Default is None.
pt2_size : float or float
size of points to plot. Default is None.
model : ortools.linear_solver.pywraplp.Solver
proxy of <Swig Object of type 'operations_research::MPSolver *'
title : str
plot title. Default is None.
figsize : tuple
Figure size for plot. Default is (12,12).
save_fig : bool
Default is False.
Returns
-------
add_to_legend : list
items to add to legend
"""
for_multiplot = True
if not fig and not base:
for_multiplot = False
fig, base = plt.subplots(1, 1, figsize=figsize)
# add title
if not for_multiplot:
if model:
title += " - " + model.name
base.set_title(title, size=20)
else:
base.set_title(model.name, size=20)
# plot non-results data
if plot_aux:
for k, df in plot_aux.items():
if k == "streets":
df.plot(ax=base, lw=2, edgecolor="k", zorder=1)
if k == "buffer":
df.plot(ax=base, facecolor="y", lw=0.25, alpha=0.25, zorder=1)
if k == "cli_tru":
if plot_res:
df = df[df[model.name + "_sol"] == "closed"]
psize = pt2_size / 6.0
pcolor = "k"
else:
n_cli = df.shape[0]
psize = pt1_size
pcolor = "r"
df.plot(ax=base, markersize=psize, edgecolor="k", facecolor=pcolor)
if k == "fac_tru":
if plot_res:
df = df[df[model.name + "_sol"] == "closed"]
psize = pt2_size
pcolor = "k"
pmarker = "*"
else:
n_cli = df.shape[0]
psize = pt1_size
pcolor = "b"
pmarker = "o"
df.plot(
ax=base,
markersize=psize,
edgecolor="k",
facecolor=pcolor,
marker=pmarker,
)
n_fac = df.shape[0]
if k == "cli_snp":
df.plot(
ax=base,
markersize=pt2_size,
edgecolor="k",
facecolor="r",
alpha=0.75,
)
if k == "fac_snp":
df.plot(
ax=base,
markersize=pt2_size,
edgecolor="k",
facecolor="b",
alpha=0.75,
)
add_to_legend = list(plot_aux.keys())
else:
add_to_legend = None
# plot results data
if plot_res:
dv_colors = dv_colorset(plot_res["fac_var"].dv)
# facilities
df = plot_res["fac_var"][plot_res["fac_var"][model.name + "_sol"] != "closed"]
alpha = 1.0 / float(len(df.dv) - 2)
if alpha > 0.5:
alpha = 0.5
# decision variable info for legend
dvs_to_leg = {}
# plot facilities
for dv in df.dv:
fac = df[df.dv == dv]
fac.plot(
ax=base,
marker="*",
markersize=pt1_size * 3.0,
alpha=0.8,
zorder=3,
edgecolor="k",
facecolor=dv_colors[dv],
)
# update decision variable info with set color
dvs_to_leg[dv] = {"facecolor": dv_colors[dv]}
# plot clients & service areas
for f, c in model.fac2cli.items():
fc = plot_res["cli_var"][plot_res["cli_var"].dv.isin(c)]
fc.plot(
ax=base,
markersize=50,
edgecolor="k",
facecolor=dv_colors[f],
alpha=alpha,
zorder=2,
)
# update decision variable info with set client counts
dvs_to_leg[f].update({"clients": fc.shape[0]})
# create service area polygon
service_area = concave_hull(df, fc, f)
service_area.plot(
ax=base, edgecolor="k", alpha=0.2, facecolor=dv_colors[f], zorder=1
)
else:
dvs_to_leg = None
if not model:
class _ShellModel:
"""object to mimic `model` when not present
"""
def __init__(self, plot_aux):
try:
self.n_cli = plot_aux["cli_tru"].shape[0]
try:
self.n_fac = plot_aux["fac_tru"].shape[0]
except KeyError:
pass
except KeyError:
pass
try:
model = _ShellModel(plot_aux)
except (TypeError, KeyError):
model = None
if not for_multiplot:
# create legend patches
patches = create_patches(
model=model,
for_multiplot=for_multiplot,
pt1_size=pt1_size,
pt2_size=pt2_size,
buffered=buffered,
legend_aux=add_to_legend,
dvs_to_leg=dvs_to_leg,
)
add_legend(patches, for_multiplot=for_multiplot)
add_north_arrow(base)
add_scale(base)
if save_fig:
plt.savefig(model.name + ".png")
# if for a multiplot explicityly return items to add to legend
if for_multiplot:
return add_to_legend
def multi_plotter(
models,
plot_aux=None,
plot_res=None,
select=None,
title=None,
figsize=(14, 14),
shape=(2, 2),
):
"""plot multiple base axes as one figure
Parameters
----------
models : list
solved model objects
select : dict
facility-to-selection count lookup.
shape : tuple
dimension for subplot array. Default is (2,2).s
plot_aux : see plotter()
plot_res : see plotter()
title : see plotter()
figsize : see plotter()
"""
pt1_size, pt2_size = 300, 60
# convert list of models to array
mdls = numpy.array(models).reshape(shape)
fig, axarr = plt.subplots(
mdls.shape[0], mdls.shape[1], figsize=figsize, sharex="col", sharey="row"
)
# add super title to subplot array
plt.suptitle(title, fontsize=30)
fig.subplots_adjust(hspace=0.1, wspace=0.005, top=0.925)
# create each subplot
for i in range(mdls.shape[0]):
for j in range(mdls.shape[1]):
add_to_legend = plotter(
base=axarr[i, j],
plot_aux=plot_aux,
plot_res=plot_res,
model=mdls[i, j],
pt1_size=pt1_size,
pt2_size=pt2_size,
)
axarr[i, j].set_aspect("equal")
add_to_legend = set(add_to_legend)
# decision variable color set
dv_colors = dv_colorset(plot_res["fac_var"].dv)
dvs_to_leg = {f: dv_colors[f] for m in models for f in m.fac2cli.keys()}
# set ordered dict of {iloc:fac_var, color, x-selected}
# *** models[0] can be any of the solved models
dvs_to_leg = {
models[0].fac2iloc[k]: (k, v, select[k]) for k, v in dvs_to_leg.items()
}
dvs_to_leg = OrderedDict(sorted(dvs_to_leg.items()))
# create legend patches
patches = create_patches(
model=None,
pt1_size=pt1_size,
pt2_size=pt2_size,
legend_aux=add_to_legend,
dvs_to_leg=dvs_to_leg,
for_multiplot=True,
)
add_legend(patches, for_multiplot=True)
def add_north_arrow(base):
"""add a north arrow to an axes
Parameters
----------
base : see plotter()
"""
arw = "rarrow, pad=0.25"
bbox_props = dict(boxstyle=arw, fc="w", ec="k", lw=2, alpha=0.75)
base.text(
221200,
267200,
" z ",
bbox=bbox_props,
fontsize="large",
fontweight="heavy",
ha="center",
va="center",
rotation=90,
)
def add_scale(base):
"""add a scale arrow to an axes
Parameters
----------
base : see plotter()
"""
bbox_props = dict(boxstyle="round, pad=.5", fc="w", ec="0.5", alpha=0.7)
base.text(
base.get_xlim()[0] + 75,
base.get_ylim()[0] + 75,
"| ~.25km~ |",
fontstyle="italic",
bbox=bbox_props,
)
def create_patches(
model=None,
pt1_size=None,
pt2_size=None,
buffered=None,
legend_aux=None,
dvs_to_leg=None,
for_multiplot=False,
):
"""create all patches to add to the legend.
Parameters
----------
for_multiplot : bool
for a single plot (True), or multiplot (False).
Default is False.
model : see plotter()
pt1_size : see plotter()
pt2_size : see plotter()
buffered : see plotter()
legend_aux : see plotter()
dvs_to_leg : see plotter()
Returns
-------
patches : list
legend handles matching plotted items
"""
if pt1_size:
ms1 = float(pt1_size) / 6.0
if pt2_size:
ms2 = float(pt2_size) / 8.0
# empty legend spacing
spacer = mpatches.Patch(edgecolor="None", facecolor="None", linewidth=0, label="")
# all patches to add to legend
patches = []
# streets -- always plot
strs = mlines.Line2D([], [], color="k", linewidth=2, alpha=1, label="Streets")
patches.extend([spacer, strs])
# non-results data
if legend_aux:
if "buffer" in legend_aux:
label = "Street buffer (%sm)" % buffered
strbuff = mpatches.Patch(
edgecolor="None", facecolor="y", linewidth=2, alpha=0.5, label=label
)
patches.extend([spacer, strbuff])
if "cli_tru" in legend_aux:
try:
if dvs_to_leg:
pcolor = "k"
msize = ms2 / 3.0
plabel = "Uncovered Households " + "($n$=%i)" % model.n_cli_uncov
else:
pcolor = "r"
msize = ms1
plabel = "Households ($n$=%i)" % model.n_cli
cli_tru = mlines.Line2D(
[],
[],
color=pcolor,
marker="o",
ms=msize,
linewidth=0,
alpha=1,
markeredgecolor="k",
label=plabel,
)
patches.extend([spacer, cli_tru])
except AttributeError:
pass
if "fac_tru" in legend_aux:
if dvs_to_leg:
pcolor = "k"
msize = ms2
pmarker = "*"
no_fac = model.n_fac - len(list(model.fac2cli.keys()))
plabel = "Unselected Facilities ($n$=%i)" % no_fac
else:
pcolor = "b"
msize = ms1
pmarker = "o"
plabel = "Little Free Library candidates" + "($n$=%i)" % model.n_fac
fac_tru = mlines.Line2D(
[],
[],
color=pcolor,
marker=pmarker,
ms=msize,
markeredgecolor="k",
linewidth=0,
alpha=1,
label=plabel,
)
patches.extend([spacer, fac_tru])
if "cli_snp" in legend_aux:
label = "Households snapped to network"
cli_snp = mlines.Line2D(
[],
[],
color="r",
marker="o",
ms=ms2,
linewidth=0,
alpha=1,
markeredgecolor="k",
label=label,
)
patches.extend([spacer, cli_snp])
if "fac_snp" in legend_aux:
label = "LFL candidates snapped to network"
fac_snp = mlines.Line2D(
[],
[],
color="b",
marker="o",
ms=ms2,
markeredgecolor="k",
linewidth=0,
alpha=1,
label=label,
)
patches.extend([spacer, fac_snp])
patches.extend([spacer])
# results data for single plot
if dvs_to_leg and not for_multiplot:
# add facility, client, and service area patches to legend
for k, v in dvs_to_leg.items():
fdv_label = "Little Free Library %s" % k
fdv = mlines.Line2D(
[],
[],
color=v["facecolor"],
marker="*",
ms=ms1 / 2.0,
markeredgecolor="k",
linewidth=0,
alpha=0.8,
label=fdv_label,
)
cdv_label = "Households served by %s " % k + "($n$=%i)" % v["clients"]
cdv = mlines.Line2D(
[],
[],
color=v["facecolor"],
marker="o",
ms=ms1 / 6.0,
markeredgecolor="k",
linewidth=0,
alpha=0.5,
label=cdv_label,
)
serv_label = "%s service area" % k
serv = mpatches.Patch(
edgecolor="k",
facecolor=v["facecolor"],
linewidth=2,
alpha=0.25,
label=serv_label,
)
patches.extend([spacer, fdv, cdv, serv, spacer])
# results data for multiplot
if dvs_to_leg and for_multiplot:
for idx, (k, v, n) in dvs_to_leg.items():
fdv = mlines.Line2D(
[],
[],
color=v,
marker="*",
ms=ms1 / 2,
markeredgecolor="k",
linewidth=0,
alpha=0.8,
label="%s ($n$=%i)" % (k, n),
)
patches.extend([spacer, fdv, spacer])
return patches
def add_legend(patches, for_multiplot=False):
"""Add a legend to a plot
Parameters
----------
patches : list
legend handles matching plotted items
for_multiplot : create_patches
"""
if for_multiplot:
anchor = (1.1, 1.65)
else:
anchor = (1.005, 1.016)
legend = plt.legend(
handles=patches,
loc="upper left",
fancybox=True,
framealpha=0.85,
bbox_to_anchor=anchor,
fontsize="x-large",
)
legend.get_frame().set_facecolor("white")
def dv_colorset(dvs):
"""decision variables color set
Parameters
---------
dvs : geopandas.GeoSeries
facility decision variables
Returns
-------
dv_colors : dict
decision variable to set color lookup
"""
dv_colors = [
"fuchsia",
"mediumseagreen",
"blueviolet",
"darkslategray",
"lightskyblue",
"saddlebrown",
"cyan",
"darkgoldenrod",
"limegreen",
"peachpuff",
"coral",
"mediumvioletred",
"darkcyan",
"thistle",
"lavender",
]
dv_colors = {dv: dv_colors[idx] for idx, dv in enumerate(dvs)}
return dv_colors
def get_buffer(in_data, buff=50):
""" geopandas.GeoDataFrame should be in a meters projection.
Parameters
----------
in_data : geopandas.GeoDataFrame
GeoDataFrame of a shapefile representing a road network.
buff : int or float
Desired buffer distance. Default is 50 (meters).
Returns
=======
out_data : geopandas.GeoDataFrame
Single polygon of the unioned street buffers.
"""
b1 = in_data.buffer(buff) # Buffer
ub = b1.unary_union # Buffer Union
b2 = geopandas.GeoSeries(ub)
out_data = geopandas.GeoDataFrame(b2, crs=in_data.crs, columns=["geometry"])
return out_data
Utilizing libpysal.cg.alpha_shapes
def concave_hull(fac_df, cli_df, f, smoother=10):
"""Create `libpysal.cg.alpha_shape_auto()` object
for service area representation.
Parameters
----------
fac_df : geopandas.GeoDataFrame
GeoDataFrame of facility locations.
cli_df : geopandas.GeoDataFrame
GeoDataFrame of client locations.
f : str
facility decision variable name.
smoother : float or int
buffer (meters). Default is 10.
Returns
-------
ccv : geopandas.GeoDataFrame
polygon representing facility service area
"""
# client location coordinates
c_array = numpy.array(
cli_df.geometry.apply(lambda pt: [pt.x, pt.y]).squeeze().tolist()
)
# facility location coordinates
f_array = numpy.array(
fac_df[fac_df.dv == f].geometry.apply(lambda pt: [pt.x, pt.y]).squeeze()
)
# coordinates of all location in the set
pts_array = numpy.vstack((c_array, f_array))
# create alpha shape (concave hull)
ccv = cg.alpha_shape_auto(pts_array, step=4)
ccv = geopandas.GeoDataFrame([ccv.buffer(smoother)], columns=["geometry"])
return ccv
def simulated_geo_points(in_data, needed=20, seed=0, to_file=None):
"""Generate synthetic spatial data points within an area.s
Parameters
----------
in_data : geopandas.GeoDataFrame
A single polygon of the unioned street buffers.
needed : int
Number of points in the buffer. Default is 20.
seed : int
Seed for pseudo-random number generation. Default is 0.
to_file : str
File name for write out.
Returns
-------
sim_pts : geopandas.GeoDataFrame
Points within the buffer.
"""
geoms = in_data.geometry
area = tuple(in_data.total_bounds)
simulated_points_list = []
simulated_points_all = False
numpy.random.seed(seed)
while simulated_points_all == False:
x = numpy.random.uniform(area[0], area[2], 1)
y = numpy.random.uniform(area[1], area[3], 1)
point = Point(x, y)
if geoms.intersects(point)[0]:
simulated_points_list.append(point)
if len(simulated_points_list) == needed:
simulated_points_all = True
sim_pts = geopandas.GeoDataFrame(
simulated_points_list, columns=["geometry"], crs=in_data.crs
)
if to_file:
sim_pts.to_file(to_file + ".shp")
return sim_pts
def analytics_matrix(mdls):
"""create stylized dataframe visualization of
distance analytics
Parameters
----------
mdls : models
all modeling scenarios
Returns
-------
df : geopandas.GeoDataFrame
distance analytics matrix
style : pandas.io.formats.style.Styler
style dataframe view
"""
model_names = [m.name for m in mdls]
boiler = " to assigned facility"
stats = {
"abs_min": "Absolute min dist" + boiler,
"abs_max": "Absolute max dist" + boiler,
"mean_means": "Mean of mean dists per client" + boiler,
"mean_stds": "Mean of StD dists per client" + boiler,
}
# instantiate dataframe
df = geopandas.GeoDataFrame()
df["stats"] = list(stats.keys())
for n in model_names:
df[n] = numpy.nan
# calculate stat for each model
for m in mdls:
mins, maxs, stds, means = [], [], [], []
for f, cs in m.fac2cli.items():
rows = numpy.array([m.cli2iloc[c] for c in cs])
col = numpy.array([m.fac2iloc[f]])
dists = m.cij[rows[:, None], col]
mins.append(dists.min()), maxs.append(dists.max()),
stds.append(dists.std()), means.append(dists.mean())
# fill cells
calcs = [
numpy.array(mins).min(),
numpy.array(maxs).max(),
numpy.array(means).mean(),
numpy.array(stds).mean(),
]
label_calc = {k: calcs[idx] for idx, k in enumerate(list(stats.keys()))}
for k, v in label_calc.items():
df.loc[(df["stats"] == k), m.name] = v
# stylize
cm = seaborn.light_palette("green", as_cmap=True, reverse=True)
style = df.style.set_caption(stats).background_gradient(
axis=1, cmap=cm, subset=model_names
)
return df, style
def selection_matrix(mdls):
"""create stylized dataframe visualization of
selected decision variables
Parameters
----------
mdls : models
all modeling scenarios
Returns
-------
df : geopandas.GeoDataFrame
variable selection matrix
style : pandas.io.formats.style.Styler
style dataframe view
"""
def _highlight_membership(s):
"""highlight set membership in pandas.DataFrame.
"""
return ["background-color: limegreen" if v == "$\in$" else "" for v in s]
# set index and coluns in empty dataframe
var_index = [v.name() for k, v in models[0].fac_vars.items()]
df = geopandas.GeoDataFrame(index=var_index, columns=[m.name for m in models])
# if site was selected in a model label with
# latex symbol for 'element of a set' ($\in$)
for m in models:
for f in df.index:
if f in list(m.fac2cli.keys()):
df.loc[f, m.name] = "$\in$"
# label all other cells with latex ($\\notin$)
df.fillna("$\\notin$", inplace=True)
for idx in df.index:
sel = df.loc[idx][df.loc[idx] == "$\in$"].shape[0]
df.loc[idx, "$\sum$"] = sel
df.loc[idx, "$\%$"] = (float(sel) / float(4)) * 100.0
# stylize
cm = seaborn.light_palette("green", as_cmap=True)
style = df.style.apply(_highlight_membership).background_gradient(
cmap=cm, subset=["$\sum$", "$\%$"]
)
return df, style
streets = geopandas.read_file(examples.get_path("streets.shp"))
streets.crs = "epsg:2223"
streets = streets.to_crs("epsg:2762")
streets.head()
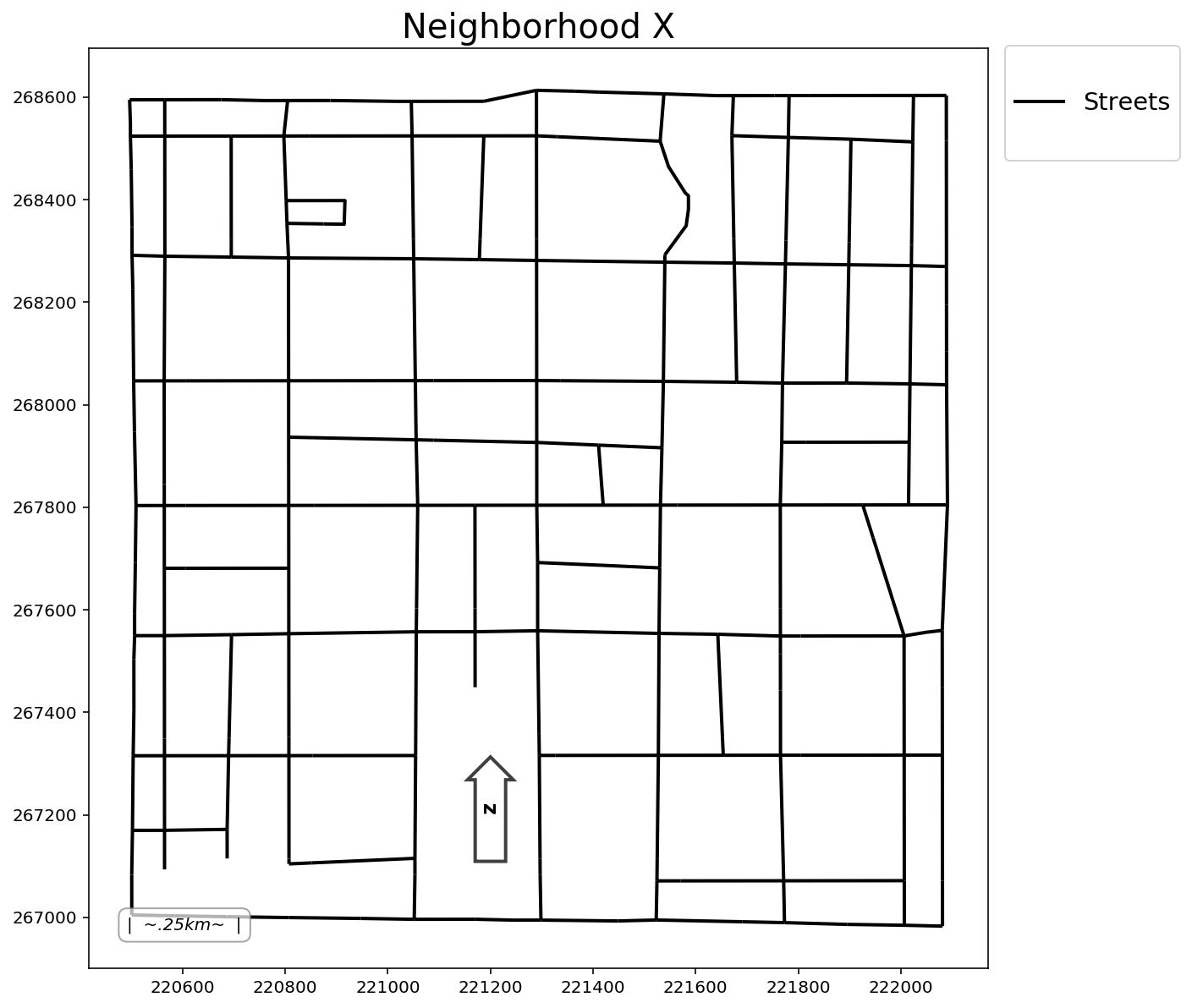
Plot
add_to_plot = {"streets": streets}
plotter(plot_aux=add_to_plot, title=title)
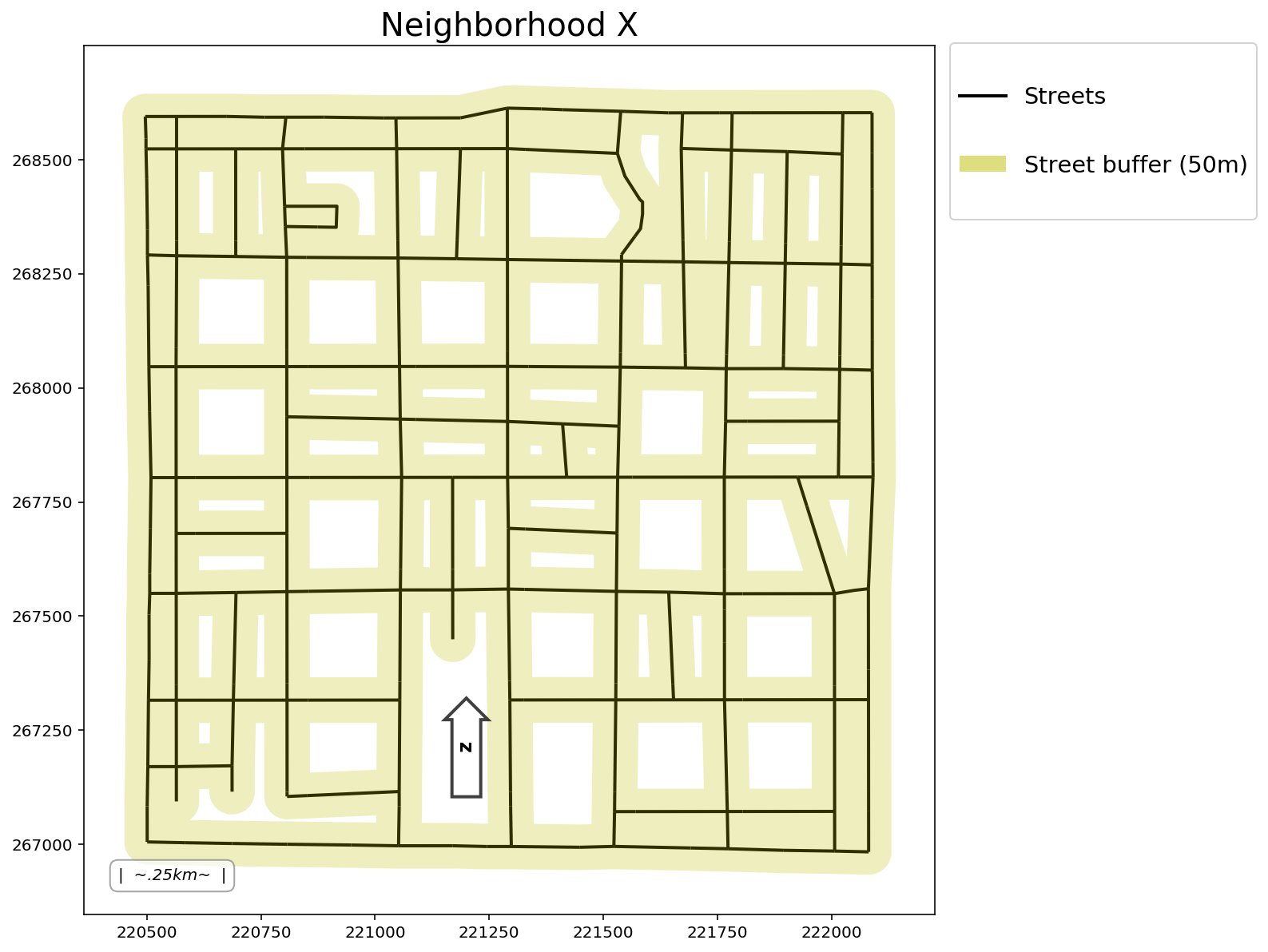
Buffer streets
buff = 50
streets_buffer = get_buffer(streets, buff=buff)
streets_buffer
Plot
add_to_plot = {"streets": streets, "buffer": streets_buffer}
plotter(plot_aux=add_to_plot, buffered=buff, title=title)
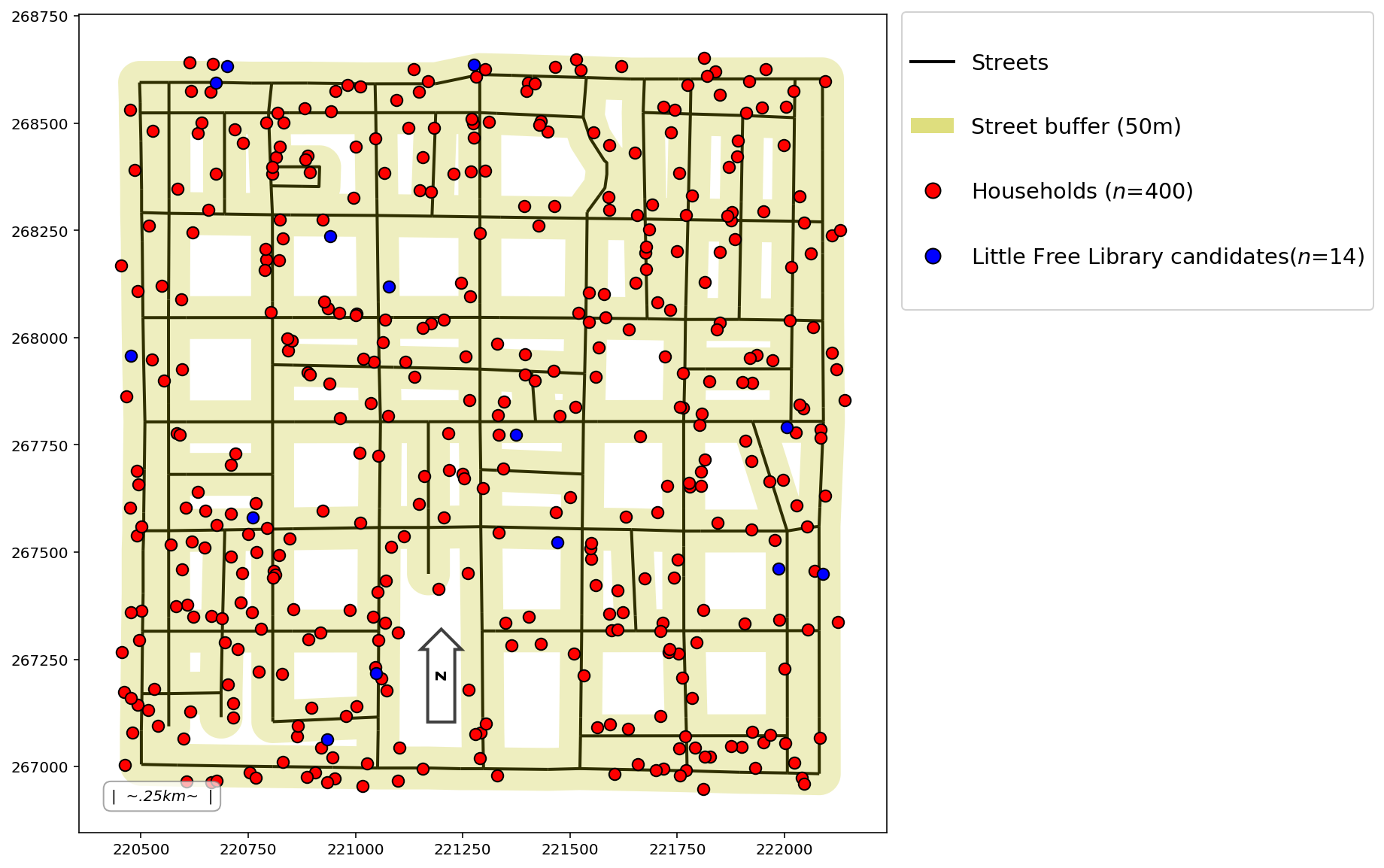
Generate synthetic client points and synthetic facility points
clients = simulated_geo_points(
streets_buffer, needed=client_count, seed=random_seeds["client"]
)
facilities = simulated_geo_points(
streets_buffer, needed=facility_count, seed=random_seeds["facility"]
)
Add decision variables to each dataset
clients["dv"] = ["x[%s]" % c for c in range(client_count)]
facilities["dv"] = ["y[%s]" % c for c in range(facility_count)]
Plot
add_to_plot = {
"streets": streets,
"buffer": streets_buffer,
"cli_tru": clients,
"fac_tru": facilities,
}
plotter(plot_aux=add_to_plot, buffered=buff, pt1_size=60)
numpy.random.seed(1991)
clients["weights"] = numpy.random.randint(1, 8, (client_count, 1))
clients.head()
ntw = spaghetti.Network(in_data=streets)
ntw.snapobservations(clients, "clients", attribute=True)
clients_snapped = spaghetti.element_as_gdf(
ntw, pp_name="clients", snapped=True
)
ntw.snapobservations(facilities, "facilities", attribute=True)
facilities_snapped = spaghetti.element_as_gdf(
ntw, pp_name="facilities", snapped=True
)
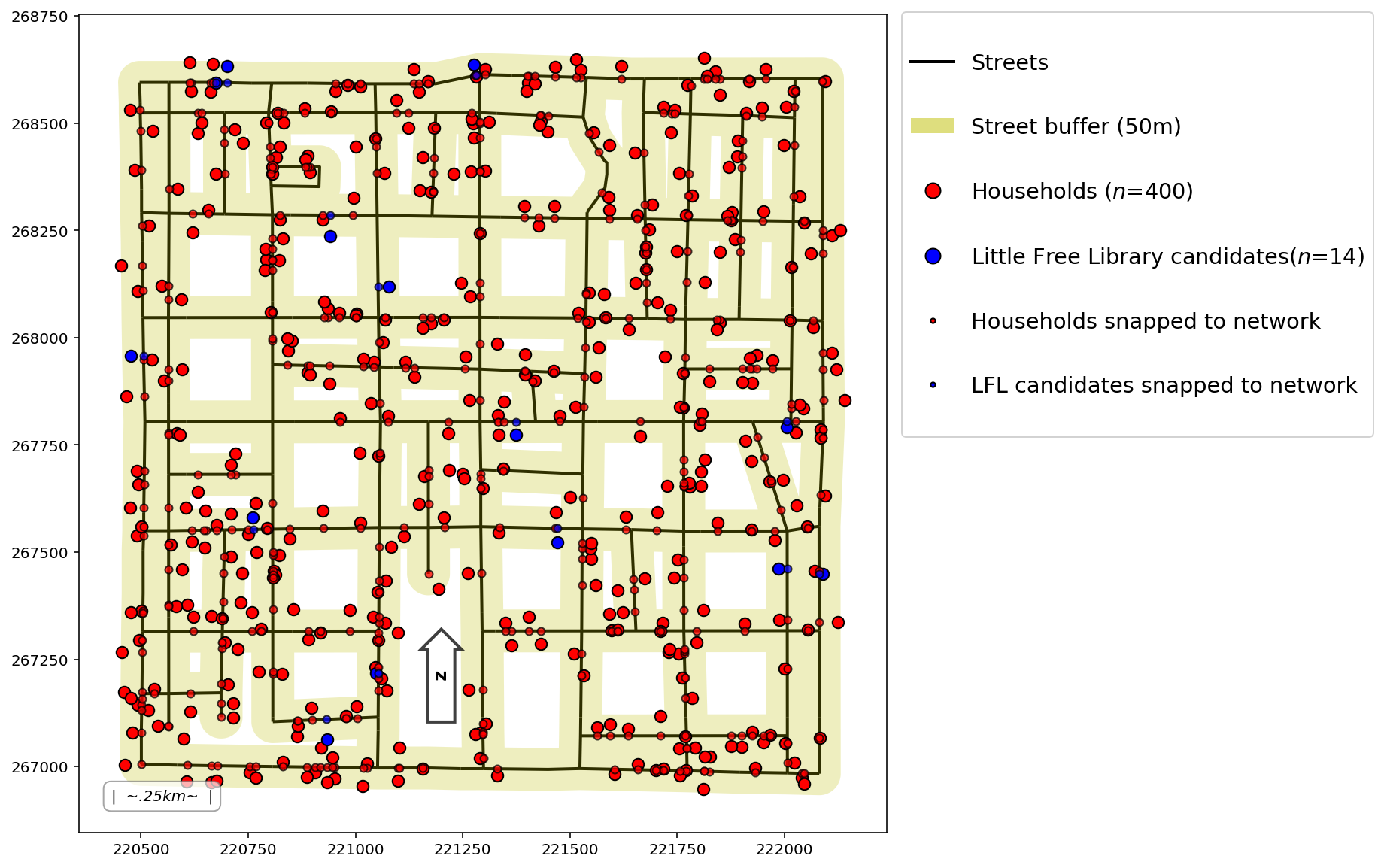
Plot
add_to_plot = {
"streets": streets,
"buffer": streets_buffer,
"cli_tru": clients,
"fac_tru": facilities,
"cli_snp": clients_snapped,
"fac_snp": facilities_snapped,
}
plotter(plot_aux=add_to_plot, buffered=buff, pt1_size=60, pt2_size=25)
cost_matrix = ntw.allneighbordistances(
sourcepattern=ntw.pointpatterns["clients"],
destpattern=ntw.pointpatterns["facilities"],
)
cost_matrix[:3, :3]
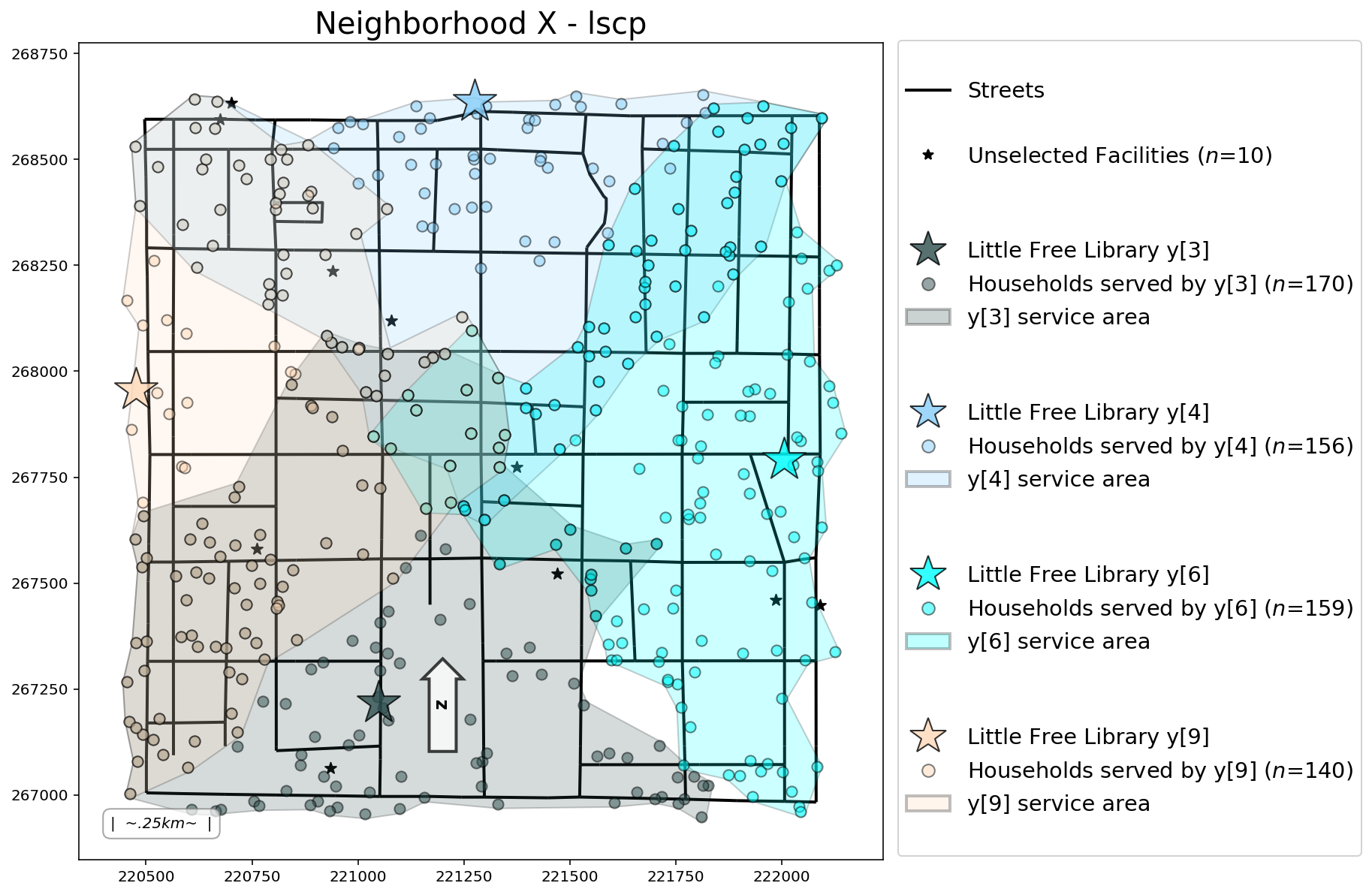
lscp = FacilityLocationModel("lscp", cij=cost_matrix, s=max_coverage)
clients, facilities = add_results(lscp, clients, facilities)
Plot
aux_to_plot = {"streets": streets, "fac_tru": facilities}
res_to_plot = {"cli_var": clients, "fac_var": facilities}
plotter(
plot_aux=aux_to_plot,
plot_res=res_to_plot,
pt1_size=300,
pt2_size=60,
model=lscp,
title=title,
)
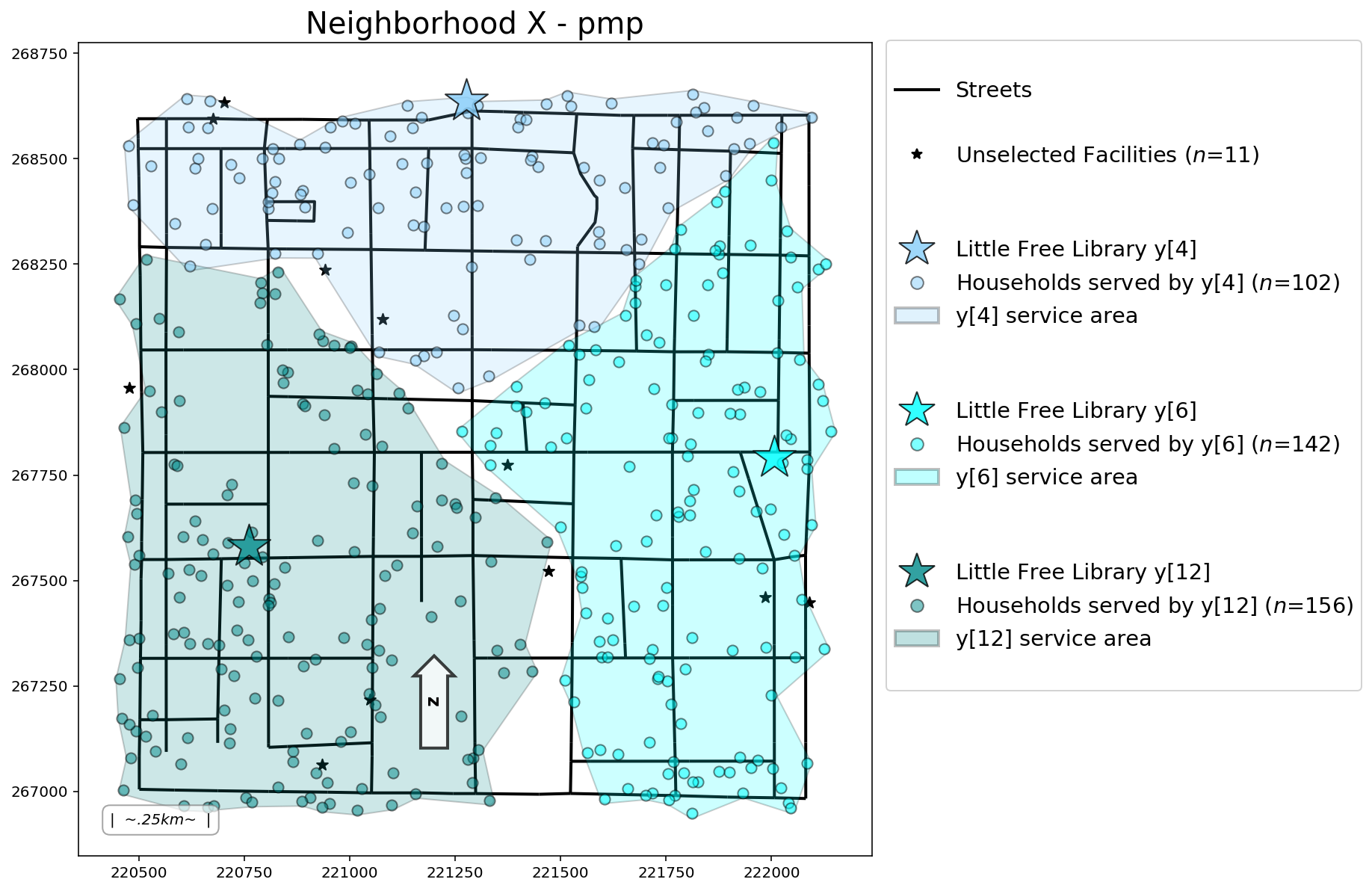
pmp = FacilityLocationModel(
"pmp", ai=clients["weights"], cij=cost_matrix, p=p_facilities
)
clients, facilities = add_results(pmp, clients, facilities)
Plot
aux_to_plot = {"streets": streets, "fac_tru": facilities}
res_to_plot = {"cli_var": clients, "fac_var": facilities}
plotter(
plot_aux=aux_to_plot,
plot_res=res_to_plot,
pt1_size=300,
pt2_size=60,
model=pmp,
title=title,
)
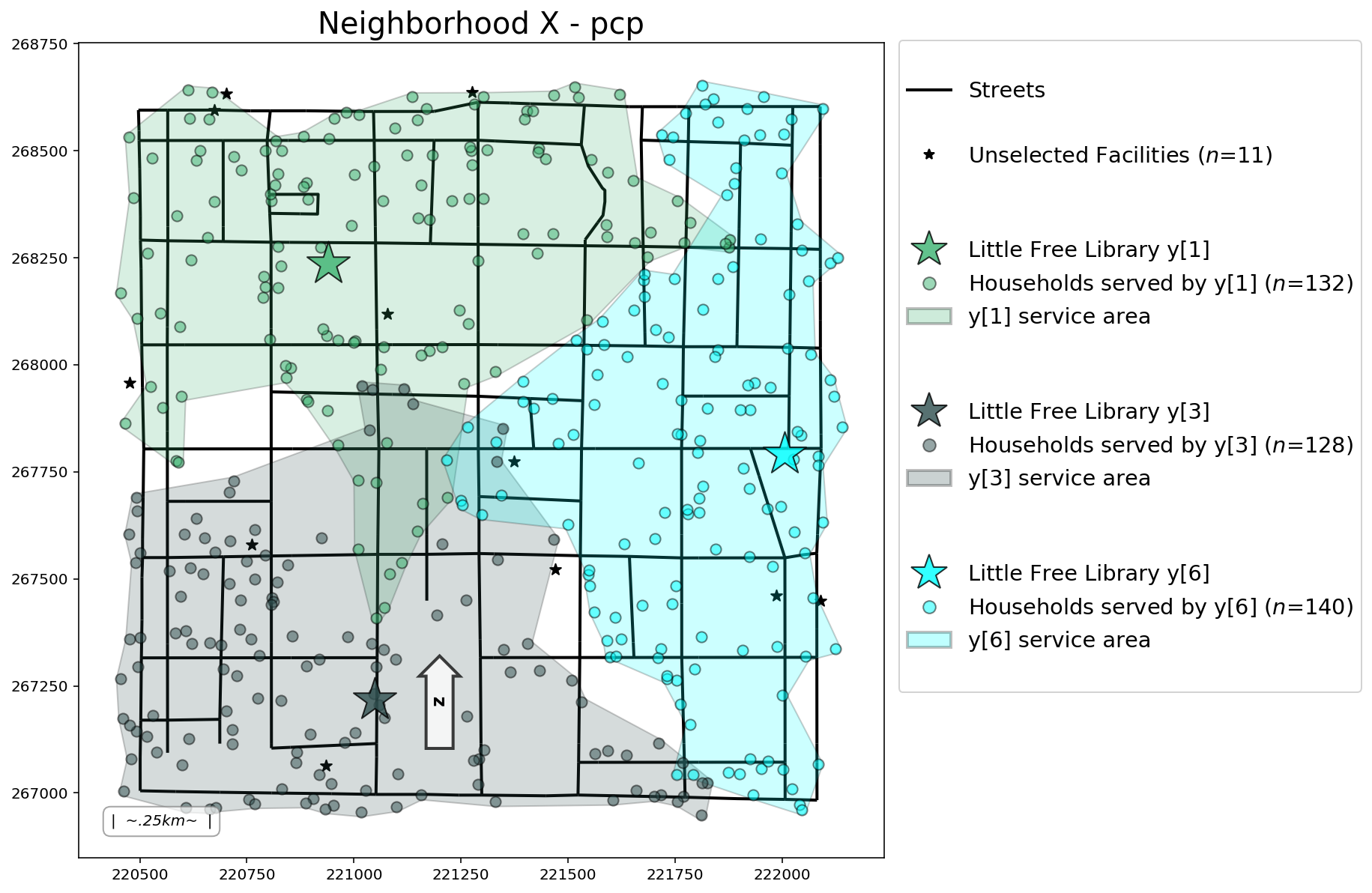
pcp = FacilityLocationModel("pcp", cij=cost_matrix, p=p_facilities)
clients, facilities = add_results(pcp, clients, facilities)
Plot
aux_to_plot = {"streets": streets, "fac_tru": facilities}
res_to_plot = {"cli_var": clients, "fac_var": facilities}
plotter(
plot_aux=aux_to_plot,
plot_res=res_to_plot,
pt1_size=300,
pt2_size=60,
model=pcp,
title=title,
)
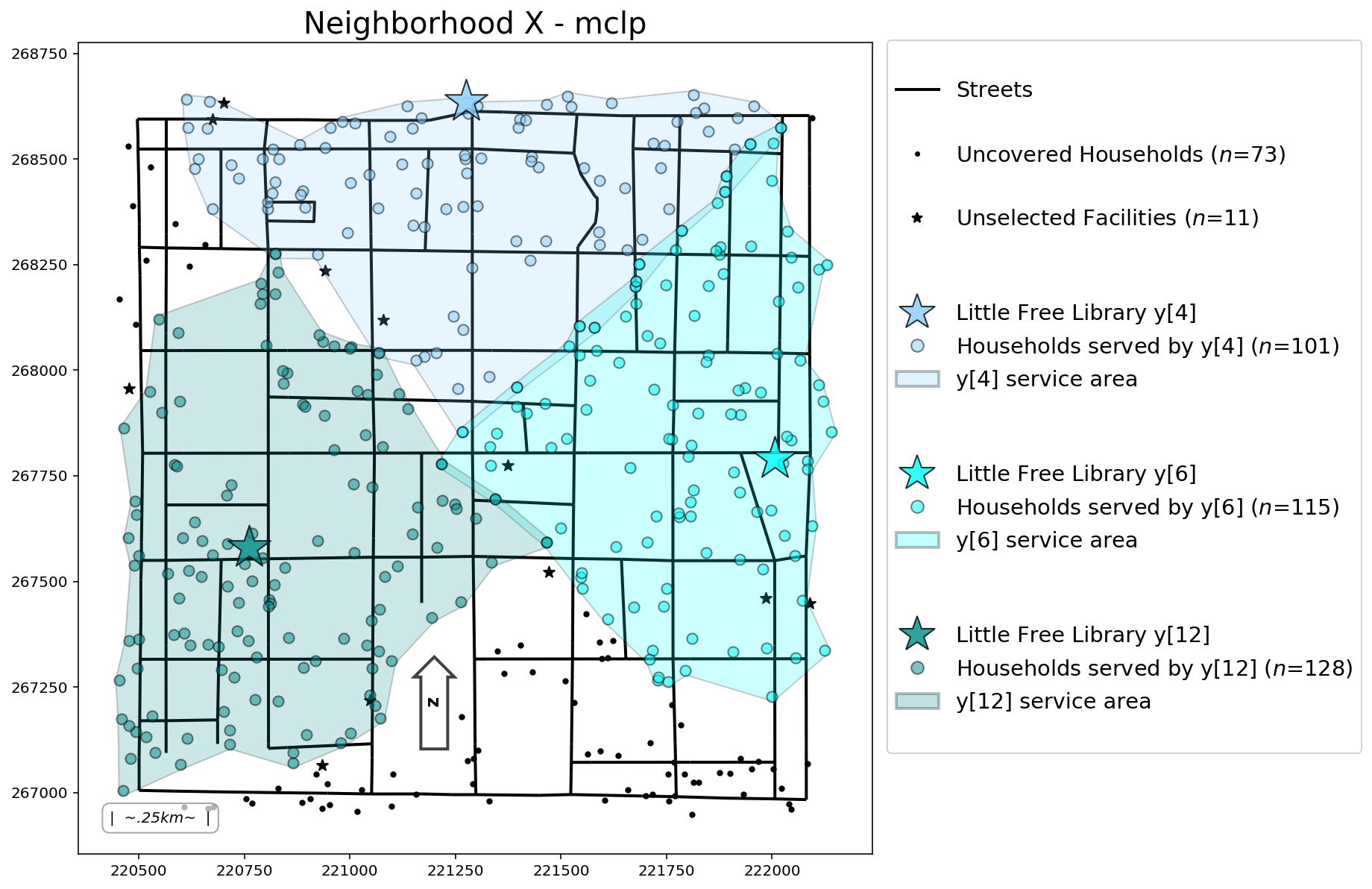
mclp = FacilityLocationModel(
"mclp", ai=clients["weights"], cij=cost_matrix, p=p_facilities, s=min_coverage
)
clients, facilities = add_results(mclp, clients, facilities)
Plot
aux_to_plot = {"streets": streets, "cli_tru": clients, "fac_tru": facilities}
res_to_plot = {"cli_var": clients, "fac_var": facilities}
plotter(
plot_aux=aux_to_plot,
plot_res=res_to_plot,
pt1_size=300,
pt2_size=60,
model=mclp,
title=title,
)
models = [lscp, pmp, pcp, mclp]
analytics_df, analytics_display = analytics_matrix(models)
analytics_display
md(f"While it appears the `{mclp.name}` performs most optimally with the least distance per stastistic, we have to remember that the `{mclp.name}` is leaving `{mclp.n_cli_uncov}` clients uncovered. Therefore, it may generally give lower maximum and average travel costs due to the uncovered client travel costs being excluded.")
selection_df, selection_display = selection_matrix(models)
selection_display
usr_warning = "The GeoDataFrame you are attempting to plot is empty"
warnings.filterwarnings("ignore", message=usr_warning)
# facility variable-to-times selected lookup
fac2selectcount = dict(selection_df["$\sum$"].astype(int))
aux_to_plot = {"streets": streets, "cli_tru": clients}
res_to_plot = {"cli_var": clients, "fac_var": facilities}
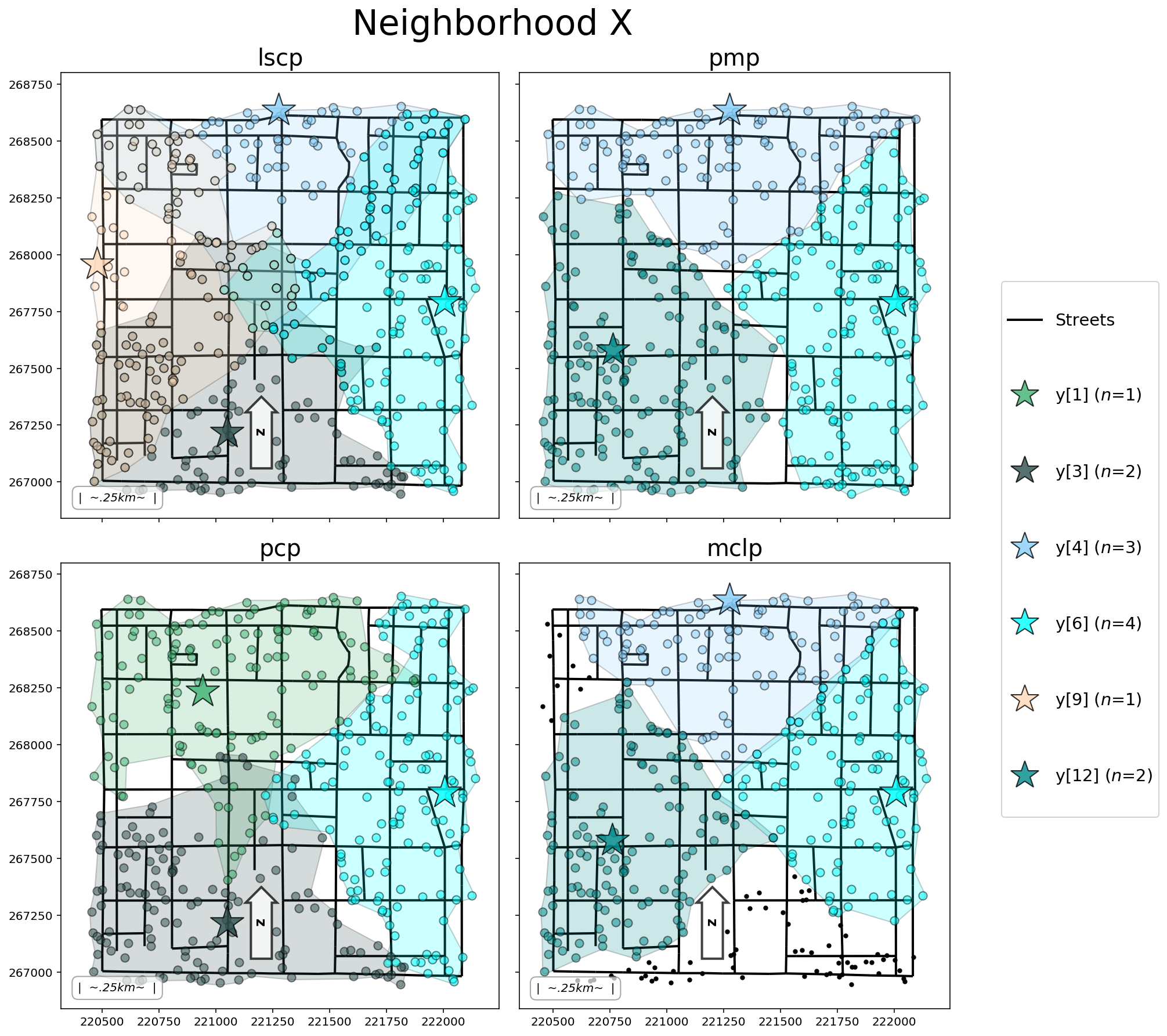
multi_plotter(
models,
plot_aux=aux_to_plot,
title=title,
plot_res=res_to_plot,
select=fac2selectcount,
)
v1 = pcp.name
v2 = str(list(pcp.fac2cli.keys())).translate({ord(r"'"): None})
v3 = analytics_df.loc[(analytics_df["stats"] == "abs_max"), "pcp"].squeeze()
v4 = max_coverage
md(f"* The `{v1}` model facility configuration: `{v2}` \n\
* This configuration results in an absolute maximum distance from any household to its assigned Little Free Library of `{v3}` meters, which is slightly more than the `{v4}` meter maximum distance stipulation put forth by the committee. Dr. Minimax believes this to be the most equitable and feasible solution for the residents of Neighbor X. However..., the Neighborhood X Planning Committee turned out to be corrupt and merely chose locations for the Little Free Libraries nearest to their respective houses....")
The open (selected) Little Free Library Locations.
facilities[facilities["pcp_sol"] != "closed"][["dv", "geometry"]]