Centrography of Point Patterns
Authors: Serge Rey sjsrey@gmail.com and Wei Kang weikang9009@gmail.com
Introduction
Centrography refers to a set of descriptive statistics that provide summary descriptions of point patterns.
This notebook introduces three types of centrography analysis for point patterns in pysal.
We also illustrate centrography analysis using two simulated datasets. See Another Example
The python file centrography.py contains several functions with which we can conduct centrography analysis.
- Central Tendency
- mean_center: calculate the mean center of the unmarked point pattern.
- weighted_mean_center: calculate the weighted mean center of the marked point pattern.
- manhattan_median: calculate the manhattan median
- euclidean_median: calculate the Euclidean median
- Dispersion and Orientation
- std_distance: calculate the standard distance
- Shape Analysis
- hull: calculate the convex hull of the point pattern
- mbr: calculate the minimum bounding box (rectangle)
All of the above functions operate on a series of coordinate pairs. That is, the data type of the first argument should be $(n,2)$ array_like. In case that you have a point pattern (PointPattern instance), you need to pass its attribute "points" instead of itself to these functions.
import numpy as np
from pointpats import PointPattern
%matplotlib inline
import matplotlib.pyplot as plt
points = [[66.22, 32.54], [22.52, 22.39], [31.01, 81.21],
[9.47, 31.02], [30.78, 60.10], [75.21, 58.93],
[79.26, 7.68], [8.23, 39.93], [98.73, 77.17],
[89.78, 42.53], [65.19, 92.08], [54.46, 8.48]]
pp = PointPattern(points) #create a point pattern "pp" from list
pp.points
type(pp.points)
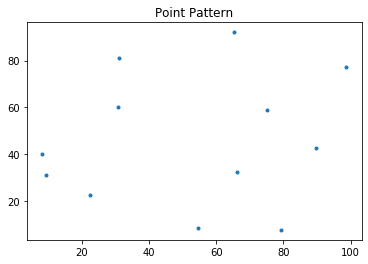
We can use PointPattern class method plot to visualize pp.
pp.plot()
#import centragraphy analysis functions
from pointpats.centrography import hull, mbr, mean_center, weighted_mean_center, manhattan_median, std_distance,euclidean_median,ellipse
Central Tendency
Central Tendency concerns about the center point of the two-dimensional distribution. It is similar to the first moment of a one-dimensional distribution. There are several ways to measure central tendency, each having pros and cons. We need to carefully select the appropriate measure according to our objective and data status.
Mean Center $(x_{mc},y_{mc})$
$$x_{mc}=\frac{1}{n} \sum^n_{i=1}x_i$$$$y_{mc}=\frac{1}{n} \sum^n_{i=1}y_i$$mc = mean_center(pp.points)
mc
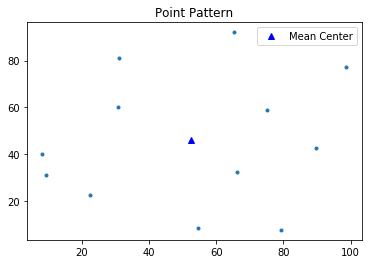
pp.plot()
plt.plot(mc[0], mc[1], 'b^', label='Mean Center')
plt.legend(numpoints=1)
Weighted Mean Center $(x_{wmc},y_{wmc})$
$$x_{wmc}=\sum^n_{i=1} \frac{w_i x_i}{\sum^n_{i=1}w_i}$$$$y_{wmc}=\sum^n_{i=1} \frac{w_i y_i}{\sum^n_{i=1}w_i}$$Weighted mean center is meant for marked point patterns. Aside from the first argument which is a seris of $(x,y)$ coordinates in weighted_mean_center function, we need to specify its second argument which is the weight for each event point.
weights = np.arange(12)
weights
wmc = weighted_mean_center(pp.points, weights)
wmc
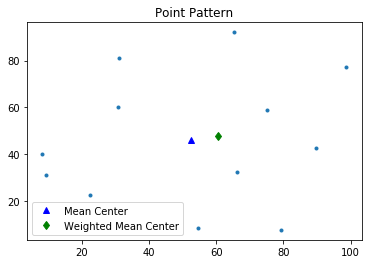
pp.plot() #use class method "plot" to visualize point pattern
plt.plot(mc[0], mc[1], 'b^', label='Mean Center')
plt.plot(wmc[0], wmc[1], 'gd', label='Weighted Mean Center')
plt.legend(numpoints=1)
Manhattan Median $(x_{mm},y_{mm})$
$$min f(x_{mm},y_{mm})= \sum^n_{i=1}(|x_i-x_{mm}|+|y_i-y_{mm}|)$$The Manhattan median is the location which minimizes the absolute distance to all the event points. It is an extension of the median measure in one-dimensional space to two-dimensional space. Since in one-dimensional space, a median is the number separating the higher half of a dataset from the lower half, we define the Manhattan median as a tuple whose first element is the median of $x$ coordinates and second element is the median of $y$ coordinates.
Though Manhattan median can be found very quickly, it is not unique if you have even number of points. In this case, pysal handles the Manhattan median the same way as numpy.median: return the average of the two middle values.
#get the number of points in point pattern "pp"
pp.n
#Manhattan Median is not unique for "pp"
mm = manhattan_median(pp.points)
mm
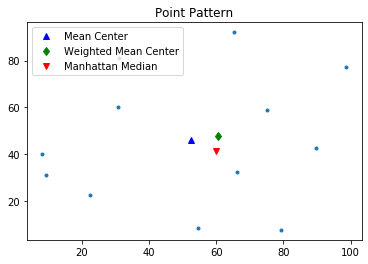
pp.plot()
plt.plot(mc[0], mc[1], 'b^', label='Mean Center')
plt.plot(wmc[0], wmc[1], 'gd', label='Weighted Mean Center')
plt.plot(mm[0], mm[1], 'rv', label='Manhattan Median')
plt.legend(numpoints=1)
Euclidean Median $(x_{em},y_{em})$
$$min f(x_{em},y_{em})= \sum^n_{i=1} \sqrt{(x_i-x_{em})^2+(y_i-y_{em})^2}$$The Euclidean Median is the location from which the sum of the Euclidean distances to all points in a distribution is a minimum. It is an optimization problem and very important for more general location allocation problems. There is no closed form solution. We can use first iterative algorithm (Kuhn and Kuenne, 1962) to approximate Euclidean Median.
Below, we define a function named median_center with the first argument points a series of $(x,y)$ coordinates and the second argument crit the convergence criterion.
def median_center(points, crit=0.0001):
points = np.asarray(points)
x0, y0 = points.mean(axis=0)
dx = np.inf
dy = np.inf
iteration = 0
while np.abs(dx) > crit or np.abs(dy) > crit:
xd = points[:, 0] - x0
yd = points[:, 1] - y0
d = np.sqrt(xd*xd + yd*yd)
w = 1./d
w = w / w.sum()
x1 = w * points[:, 0]
x1 = x1.sum()
y1 = w * points[:, 1]
y1 = y1.sum()
dx = x1 - x0
dy = y1 - y0
iteration +=1
print(x0, x1, dx, dy, d.sum(), iteration)
x0 = x1
y0 = y1
return x1, y1
median_center(pp.points, crit=.0001)
After 18 iterations, the convergence criterion is reached. The Euclidean Median is $(54.167594287646125,44.424308658832047)$.
We can also call the function euclidean_median in pysal to calculate the Euclidean Median.
em = euclidean_median(pp.points)
em
The two results we get from euclidean_median function in pysal and the median_center function we define here are very much the same.
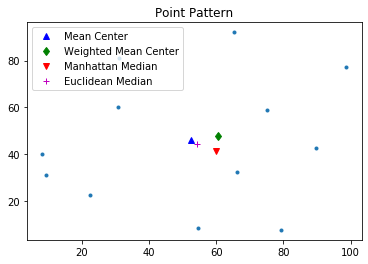
pp.plot()
plt.plot(mc[0], mc[1], 'b^', label='Mean Center')
plt.plot(wmc[0], wmc[1], 'gd', label='Weighted Mean Center')
plt.plot(mm[0], mm[1], 'rv', label='Manhattan Median')
plt.plot(em[0], em[1], 'm+', label='Euclidean Median')
plt.legend(numpoints=1)
Dispersion and Orientation
Standard Distance & Standard Distance Circle
$$SD = \displaystyle \sqrt{\frac{\sum^n_{i=1}(x_i-x_{m})^2}{n} + \frac{\sum^n_{i=1}(y_i-y_{m})^2}{n}}$$The Standard distance is closely related to the usual definition of the standard deviation of a data set, and it provides a measure of how dispersed the events are around their mean center $(x_m,y_m)$. Taken together, these measurements can be used to plot a summary circle (standard distance circle) for the point pattern, centered at $(x_m,y_m)$ with radius $SD$, as shown below.
stdd = std_distance(pp.points)
stdd
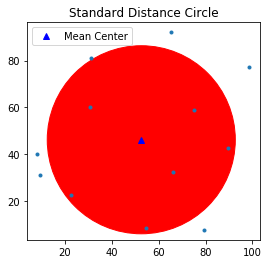
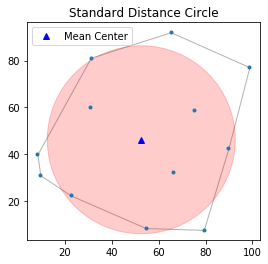
Plot mean center as well as the standard distance circle.
circle1=plt.Circle((mc[0], mc[1]),stdd,color='r')
ax = pp.plot(get_ax=True, title='Standard Distance Circle')
ax.add_artist(circle1)
plt.plot(mc[0], mc[1], 'b^', label='Mean Center')
ax.set_aspect('equal')
plt.legend(numpoints=1)
From the above figure, we can observe that there are five points outside the standard distance circle which are potential outliers.
Standard Deviational Ellipse
Compared with standard distance circle which measures dispersion using a single parameter $SD$, standard deviational ellipse measures dispersion and trend in two dimensions through angle of rotation $\theta$, dispersion along major axis $s_x$ and dispersion along minor axis $s_y$:
- Major axis defines the direction of maximum spread in the distribution. $s_x$ is the semi-major axis (half the length of the major axis):
- Minor axis defines the direction of minimum spread and is orthogonal to major axis. $s_y$ is the semi-minor axis (half the length of the minor axis):
- The ellipse is rotated clockwise through an angle $\theta$:
sx, sy, theta = ellipse(pp.points)
sx, sy, theta
theta_degree = np.degrees(theta) #need degree of rotation to plot the ellipse
theta_degree
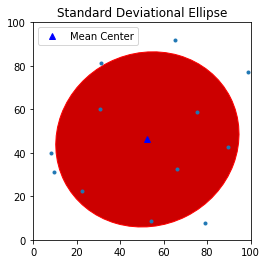
The Standard Deviational Ellipse for the point pattern is rotated clockwise by $63.25^{\circ}$.
from matplotlib.patches import Ellipse
from pylab import figure, show,rand
fig = figure()
#ax = fig.add_subplot(111, aspect='equal')
e = Ellipse(xy=mean_center(pp.points), width=sx*2, height=sy*2, angle=-theta_degree) #angle is rotation in degrees (anti-clockwise)
ax = pp.plot(get_ax=True, title='Standard Deviational Ellipse')
ax.add_artist(e)
e.set_clip_box(ax.bbox)
e.set_facecolor([0.8,0,0])
e.set_edgecolor([1,0,0])
ax.set_xlim(0,100)
ax.set_ylim(0,100)
ax.set_aspect('equal')
plt.plot(mc[0], mc[1], 'b^', label='Mean Center')
plt.legend(numpoints=1)
show()
Convex Hull
The convex hull of a point pattern pp is the smallest convex set that contains pp. We can call function hull to caculate the convex hull.
hull(pp.points)
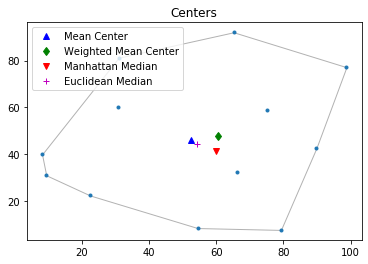
By specifying "hull" argument True in PointPattern class method plot, we can easily plot convex hull of the point pattern.
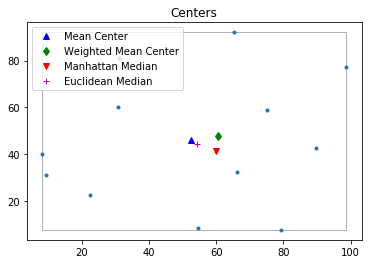
pp.plot(title='Centers', hull=True ) #plot point pattern "pp" as well as its convex hull
plt.plot(mc[0], mc[1], 'b^', label='Mean Center')
plt.plot(wmc[0], wmc[1], 'gd', label='Weighted Mean Center')
plt.plot(mm[0], mm[1], 'rv', label='Manhattan Median')
plt.plot(em[0], em[1], 'm+', label='Euclidean Median')
plt.legend(numpoints=1)
Minimum Bounding Rectangle
Minimum Bounding Rectangle (Box) is the same as the minimum bounding Rectangle of its convex hull. Thus, it is almost always bigger than convex hull.
We can call mbr function to calculate the leftmost, downmost, rightmost, and upmost value of the vertices of minimum bounding rectangle.
mbr(pp.points)
Thus, four vertices of the minimum bounding rectangle is $(8.23,7.68),(98.73,7.68),(98.73,92.08),(8.23,92.08)$.
pp.plot(title='Centers', window=True ) #plot point pattern "pp" as well as its Minimum Bounding Rectangle
plt.plot(mc[0], mc[1], 'b^', label='Mean Center')
plt.plot(wmc[0], wmc[1], 'gd', label='Weighted Mean Center')
plt.plot(mm[0], mm[1], 'rv', label='Manhattan Median')
plt.plot(em[0], em[1], 'm+', label='Euclidean Median')
plt.legend(numpoints=1)
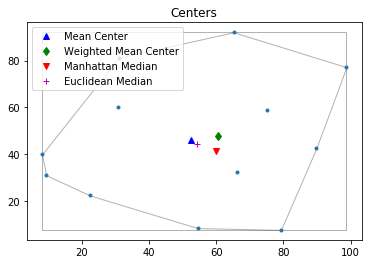
pp.plot(title='Centers', hull=True , window=True )#plot point pattern "pp", convex hull, and Minimum Bounding Rectangle
plt.plot(mc[0], mc[1], 'b^', label='Mean Center')
plt.plot(wmc[0], wmc[1], 'gd', label='Weighted Mean Center')
plt.plot(mm[0], mm[1], 'rv', label='Manhattan Median')
plt.plot(em[0], em[1], 'm+', label='Euclidean Median')
plt.legend(numpoints=1)
Plot Standard Distance Circle and Convex Hull.
circle1=plt.Circle((mc[0], mc[1]),stdd,color='r',alpha=0.2)
ax = pp.plot(get_ax=True, title='Standard Distance Circle', hull=True)
ax.add_artist(circle1)
plt.plot(mc[0], mc[1], 'b^', label='Mean Center')
ax.set_aspect('equal')
plt.legend(numpoints=1)
#from pysal.contrib import shapely_ext
from libpysal.cg import shapely_ext
from pointpats import PoissonPointProcess as csr
import libpysal as ps
from pointpats import as_window
#import pysal_examples
# open "vautm17n" polygon shapefile
va = ps.io.open(ps.examples.get_path("vautm17n.shp"))
# Create the exterior polygons for VA from the union of the county shapes
polys = [shp for shp in va]
state = shapely_ext.cascaded_union(polys)
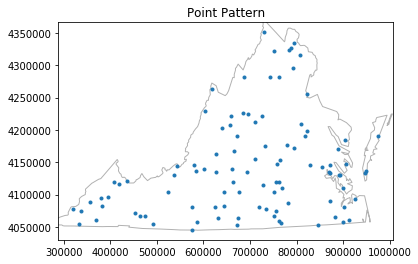
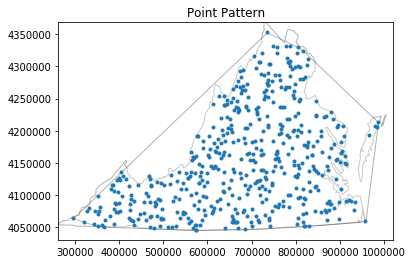
pp = csr(as_window(state), 100, 1, asPP=True).realizations[0]
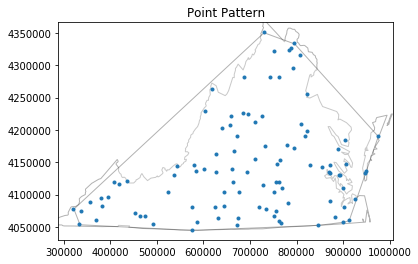
pp.plot(window=True)
pp.plot(window=True, hull=True)
mc = mean_center(pp.points)
mm = manhattan_median(pp.points)
em = euclidean_median(pp.points)
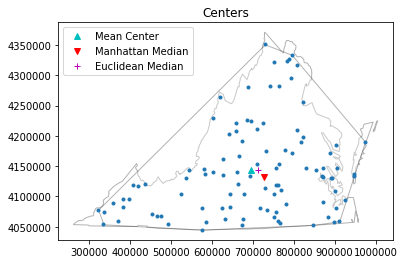
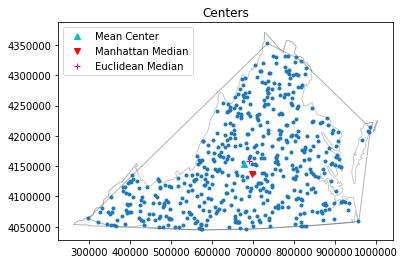
pp.plot(title='Centers', hull=True , window=True )#plot point pattern "pp", convex hull, and Minimum Bounding Rectangle
plt.plot(mc[0], mc[1], 'c^', label='Mean Center')
plt.plot(mm[0], mm[1], 'rv', label='Manhattan Median')
plt.plot(em[0], em[1], 'm+', label='Euclidean Median')
plt.legend(numpoints=1)
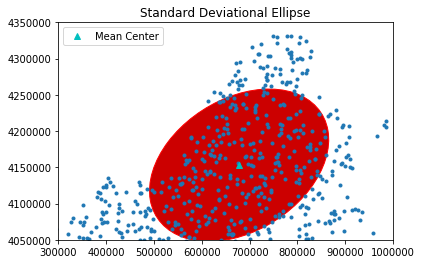
Plot Standard Distance Circle of the simulated point pattern.
sx, sy, theta = ellipse(pp.points)
sx, sy, theta
theta_degree = np.degrees(theta) #need degree of rotation to plot the ellipse
from matplotlib.patches import Ellipse
from pylab import figure, show,rand
fig = figure()
#ax = fig.add_subplot(111, aspect='equal')
e = Ellipse(xy=mean_center(pp.points), width=sx*2, height=sy*2, angle=-theta_degree)
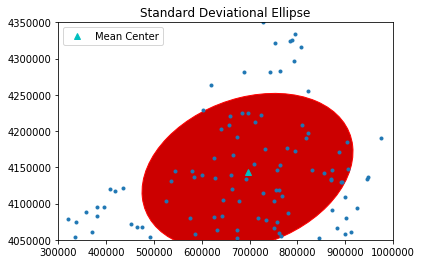
ax = pp.plot(get_ax=True, title='Standard Deviational Ellipse')
ax.add_artist(e)
e.set_clip_box(ax.bbox)
e.set_facecolor([0.8,0,0])
e.set_edgecolor([1,0,0])
ax.set_xlim(300000,1000000)
ax.set_ylim(4050000,4350000)
#ax.set_aspect('equal')
plt.plot(mc[0], mc[1], 'c^', label='Mean Center')
plt.legend(numpoints=1)
show()
pp = csr(as_window(state), 500, 1, asPP=True).realizations[0]
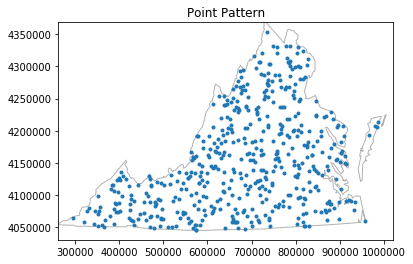
pp.plot(window=True)
pp.plot(window=True, hull=True)
mc = mean_center(pp.points)
mm = manhattan_median(pp.points)
em = euclidean_median(pp.points)
pp.plot(title='Centers', hull=True , window=True )#plot point pattern "pp", convex hull, and Minimum Bounding Rectangle
plt.plot(mc[0], mc[1], 'c^', label='Mean Center')
plt.plot(mm[0], mm[1], 'rv', label='Manhattan Median')
plt.plot(em[0], em[1], 'm+', label='Euclidean Median')
plt.legend(numpoints=1)
sx, sy, theta = ellipse(pp.points)
sx, sy, theta
theta_degree = np.degrees(theta) #need degree of rotation to plot the ellipse
from matplotlib.patches import Ellipse
from pylab import figure, show,rand
fig = figure()
#ax = fig.add_subplot(111, aspect='equal')
e = Ellipse(xy=mean_center(pp.points), width=sx*2, height=sy*2, angle=-theta_degree)
ax = pp.plot(get_ax=True, title='Standard Deviational Ellipse')
ax.add_artist(e)
e.set_clip_box(ax.bbox)
e.set_facecolor([0.8,0,0])
e.set_edgecolor([1,0,0])
ax.set_xlim(300000,1000000)
ax.set_ylim(4050000,4350000)
#ax.set_aspect('equal')
plt.plot(mc[0], mc[1], 'c^', label='Mean Center')
plt.legend(numpoints=1)
show()
If we calculate the Euclidean distances between every event point and Mean Center (Euclidean Median), and sum them up, we can see that Euclidean Median is the optimal point in iterms of minimizing the Euclidean distances to all the event points.
from pointpats import dtot
print(dtot(mc, pp.points))
print(dtot(em, pp.points))
print(dtot(mc, pp.points) > dtot(em, pp.points))