This page was generated from notebooks/tsp.ipynb.
Interactive online version:
If any part of this notebook is used in your research, please cite with the reference found in README.md.
The Traveling Sales(man)(person) Problem — TSP¶
Integrating pysal/spaghetti and pulp for optimal routing¶
Author: James D. Gaboardi jgaboardi@gmail.com
This notebook provides a use case for:
Introducing the TSP
Declaration of a solution class and model parameters
Solving the TSP for an optimal tour
[1]:
%config InlineBackend.figure_format = "retina"
[2]:
%load_ext watermark
%watermark
Last updated: 2022-11-01T23:09:28.066937-04:00
Python implementation: CPython
Python version : 3.10.6
IPython version : 8.6.0
Compiler : Clang 13.0.1
OS : Darwin
Release : 22.1.0
Machine : x86_64
Processor : i386
CPU cores : 8
Architecture: 64bit
[3]:
import geopandas
from libpysal import examples
import matplotlib
import matplotlib_scalebar
from matplotlib_scalebar.scalebar import ScaleBar
import numpy
import pulp
import spaghetti
%matplotlib inline
%watermark -w
%watermark -iv
Watermark: 2.3.1
json : 2.0.9
matplotlib : 3.6.1
matplotlib_scalebar: 0.8.0
numpy : 1.23.4
pulp : 2.6.0
libpysal : 4.6.2
spaghetti : 1.6.8
geopandas : 0.12.1
/Users/the-gaboardi/miniconda3/envs/py310_spgh_dev/lib/python3.10/site-packages/spaghetti/network.py:39: FutureWarning: The next major release of pysal/spaghetti (2.0.0) will drop support for all ``libpysal.cg`` geometries. This change is a first step in refactoring ``spaghetti`` that is expected to result in dramatically reduced runtimes for network instantiation and operations. Users currently requiring network and point pattern input as ``libpysal.cg`` geometries should prepare for this simply by converting to ``shapely`` geometries.
warnings.warn(f"{dep_msg}", FutureWarning)
1 Introduction¶
Scenario¶
Detective George B. Königsberg thought he needed to visit 7 crimes scenes in one area of City X this afternoon in order to collect evidence. However, his lieutenant, Anna Nagurney just told him he needs to double that to 14. He really wants to wrap up early so he can get home to watch the 2012 mathematical thriller, Travelling Salesman by Timothy Lanzone, with his cat and dog, Euler and Hamilton. Therefore, he decides on calculating an optimal route so that he can visit all 14 crime scenes in one tour while covering the shortest distance. Det. Königsberg utilizes an integer linear programming formulation of the traveling salesperson problem (TSP) to find his best route.
Integer Linear Programming Formulation based on Miller, Tucker, and Zemlin (1960).¶
\(\begin{array} \displaystyle \normalsize \textrm{Minimize} & \displaystyle \normalsize \sum_{0 \leq i \\ i \neq j}^n \sum_{j \leq n \\ j \neq i}^n c_{ij}x_{ij} & & & & \normalsize (1) \\ \normalsize \textrm{Subject To} & \displaystyle \normalsize \sum_{i=0}^n x_{ij}=1 & \normalsize j=1,...,n, & \normalsize j\neq i; & &\normalsize (2)\\ & \displaystyle \normalsize \sum_{j=0}^n x_{ij}=1 & \normalsize i=1,...,n, & \normalsize i\neq j; & &\normalsize (3) \\ & \displaystyle \normalsize u_i - u_j + p x_{ij} \leq p - 1 & \normalsize i=1,...,n, & \normalsize 1 \leq i \neq j \leq n; & &\normalsize (4) \\ & \normalsize x_{ij} \in \{0,1\} & \normalsize i=1,...,n, & \normalsize j=1,...,n; & &\normalsize (5)\\ & \normalsize u_{i} \in \mathbb{Z} & \normalsize i=1,...,n. & & &\normalsize (6)\\ \end{array}\)
:math:`begin{array} displaystyle normalsize textrm{Where} & small x_{ij} & small = & small begin{cases}
1, & textrm{if node } i textrm{ immediately precedes node } j textrm{ in the tour}\ 0, & textrm{otherwise}
end{cases} &&&&\
& small c_{ij} & small = & small textrm{distance matrix between all } i,j textrm{ pairs} &&&& \ & small n & small = & small textrm{the total number of nodes in the tour} &&&&\ & small i & small = & small textrm{each potential origin node} &&&&\ & small j & small = & small textrm{each potential destination node} &&&&\ & small u_i & small = & small textrm{continuous, non-negative real numbers} &&&&\ & small p & small = & small textrm{allowed visits prior to return (}n = p textrm{ in this formulation)} &&&&\ end{array}`
References
Cummings, N. (2000) A brief History of the Travelling Salesman Problem. The Operational Research Society. Accessed: 01/2020.
Dantzig, G., Fulkerson, R., and Johnson, S. (1954) Solution of a Large-Scale Traveling-Salesman Problem. Journal of the Operational Research Society of America. 2(4)393-410.
Flood, Merrill M. (1956) The Traveling-Salesman Problem. 4(1)61-75.
Gass, S. I. and Assad, A. A. (2005) An Annotated Timeline of Operations Research: An Informal History. Springer US.
Miller, C. E., Tucker, A. W., and Zemlin, R. A. (1960) Integer Programming Formulation of Traveling Salesman Problems. Journal of Association for Computing Machinery. 7(4)326-329.
Miller, H. J. and Shaw, S.-L. (2001) Geographic Information Systems for Transportation: Principles and Applications. New York. Oxford University Press.
Nemhauser, G. L. and Wolsey, L. A. (1988) Integer and Combinatorial Optimization. John Wiley & Sons, Inc.
2. A model, data and parameters¶
Solution class¶
[4]:
class MTZ_TSP:
def __init__(self, nodes, cij, xij_tag="x_%s,%s", ui_tag="u_%s", display=True):
"""Instantiate and solve the Traveling Salesperson Problem (TSP)
based the formulation from Miller, Tucker, and Zemlin (1960).
Parameters
----------
nodes : geopandas.GeoSeries
All nodes to be visited in the tour.
cij : numpy.array
All-to-all distance matrix for nodes.
xij_tag : str
Tour decision variable names within the model. Default is
'x_%s,%s' where %s indicates string formatting.
ui_tag : str
Arbitrary real number decision variable names within the model.
Default is 'u_%s' where %s indicates string formatting.
display : bool
Print out solution results.
Attributes
----------
nodes : geopandas.GeoSeries
See description in above.
p : int
The number of nodes in the set.
rp_0n : range
Range of node IDs in ``nodes`` from 0,...,``p``.
rp_1n : range
Range of node IDs in ``nodes`` from 1,...,``p``.
id : str
Column name for ``nodes``.
cij : numpy.array
See description in above.
xij_tag : str
See description in above.
ui_tag : str
See description in above.
tsp : pulp.LpProblem
Integer Linear Programming problem instance.
xij : numpy.array
Binary tour decision variables (``pulp.LpVariable``).
ui : numpy.array
Continuous arbitrary real number decision variables
(``pulp.LpVariable``).
cycle_ods : dict
Cycle origin-destination lookup keyed by origin with
destination as the value.
tour_pairs : list
OD pairs comprising each abstract tour arc.
"""
# all nodes to be visited and the distance matrix
self.nodes, self.cij = nodes, cij
# number of nodes in the set
self.p = self.nodes.shape[0]
# full and truncated range of nodes (p) in the set
self.rp_0n, self.rp_1n = range(self.p), range(1, self.p)
# column name for node IDs
self.id = self.nodes.name
# alpha tag for decision and dummy variable prefixes
self.xij_tag, self.ui_tag = xij_tag, ui_tag
# instantiate a model
self.tsp = pulp.LpProblem("MTZ_TSP", pulp.LpMinimize)
# create and set the tour decision variables
self.tour_dvs()
# create and set the arbitraty real number decision variables
self.arn_dvs()
# set the objective function
self.objective_func()
# node entry constraints
self.entry_exit_constrs(entry=True)
# node exit constraints
self.entry_exit_constrs(entry=False)
# subtour prevention constraints
self.prevent_subtours()
# solve
self.tsp.solve(pulp.PULP_CBC_CMD(msg=False))
# origin-destination lookup
self.get_decisions(display=display)
# extract the sequence of nodes to construct the optimal tour
self.construct_tour()
def tour_dvs(self):
"""Create the tour decision variables - eq (5)."""
def _name(_x):
"""Helper for naming variables"""
return self.nodes[_x].split("_")[-1]
xij = numpy.array(
[
[
pulp.LpVariable(self.xij_tag % (_name(i), _name(j)), cat="Binary")
for j in self.rp_0n
]
for i in self.rp_0n
]
)
self.xij = xij
def arn_dvs(self):
"""Create arbitrary real number decision variables - eq (6)."""
ui = numpy.array(
[pulp.LpVariable(self.ui_tag % (i), lowBound=0) for i in self.rp_0n]
)
self.ui = ui
def objective_func(self):
"""Add the objective function - eq (1)."""
self.tsp += pulp.lpSum(
[
self.cij[i, j] * self.xij[i, j]
for i in self.rp_0n
for j in self.rp_0n
if i != j
]
)
def entry_exit_constrs(self, entry=True):
"""Add entry and exit constraints - eq (2) and (3)."""
if entry:
for i in self.rp_0n:
self.tsp += (
pulp.lpSum([self.xij[i, j] for j in self.rp_0n if i != j]) == 1
)
# exit constraints
else:
for j in self.rp_0n:
self.tsp += (
pulp.lpSum([self.xij[i, j] for i in self.rp_0n if i != j]) == 1
)
def prevent_subtours(self):
"""Add subtour prevention constraints - eq (4)."""
for i in self.rp_1n:
for j in self.rp_1n:
if i != j:
self.tsp += (
self.ui[i] - self.ui[j] + self.p * self.xij[i, j] <= self.p - 1
)
def get_decisions(self, display=True):
"""Fetch the selected decision variables."""
cycle_ods = {}
for var in self.tsp.variables():
if var.name.startswith(self.ui_tag[0]):
continue
if var.varValue > 0:
if display:
print("%s: %s" % (var.name, var.varValue))
od = var.name.split("_")[-1]
o, d = [int(tf) for tf in od.split(",")]
cycle_ods[o] = d
if display:
print("Status: %s" % pulp.LpStatus[self.tsp.status])
self.cycle_ods = cycle_ods
def construct_tour(self):
"""Construct the tour."""
tour_pairs = []
for origin in self.rp_0n:
tour_pairs.append([])
try:
tour_pairs[origin].append(next_origin)
next_origin = self.cycle_ods[next_origin]
tour_pairs[origin].append(next_origin)
except NameError:
next_origin = self.cycle_ods[origin]
tour_pairs[origin].append(origin)
tour_pairs[origin].append(next_origin)
tour_pairs = {idx: sorted(tp) for idx, tp in enumerate(tour_pairs)}
self.tour_pairs = tour_pairs
def extract_tour(self, paths, id_col, leg_label="leg"):
"""Extract the tour (the legs in the journey) as a
``geopandas.GeoDataFrame`` of ``shapely.geometry.LineString`` objects.
Parameters
----------
paths : geopandas.GeoDataFrame
Shortest-path routes between all observations.
id_col : str
ID column name.
leg_label : str
Column name for the tour sequence. Default is 'leg'.
Returns
-------
tour : geopandas.GeoDataFrame
Optimal tour of ``self.nodes`` sequenced by ``leg_label`` that
retains the original index of ``paths``.
"""
paths[leg_label] = int
# set label of journey leg for each OD pair.
for leg, tp in self.tour_pairs.items():
paths.loc[paths[id_col] == tuple(tp), leg_label] = leg
# extract only paths in the tour
tour = paths[paths[leg_label] != int].copy()
tour.sort_values(by=[leg_label], inplace=True)
tour[leg_label] = tour[leg_label].astype(int)
return tour
Streets¶
[5]:
streets = geopandas.read_file(examples.get_path("streets.shp"))
streets.crs = "esri:102649"
streets = streets.to_crs("epsg:2762")
streets.head()
[5]:
| ID | Length | geometry | |
|---|---|---|---|
| 0 | 1.0 | 244.116229 | LINESTRING (222007.131 267348.711, 222007.159 ... |
| 1 | 2.0 | 375.974828 | LINESTRING (222006.951 267549.880, 222007.131 ... |
| 2 | 3.0 | 400.353405 | LINESTRING (221420.428 267804.889, 221411.402 ... |
| 3 | 4.0 | 660.000000 | LINESTRING (220875.116 268353.388, 220803.948 ... |
| 4 | 5.0 | 660.000000 | LINESTRING (220802.426 268398.824, 220917.000 ... |
Crimes¶
[6]:
all_crimes = geopandas.read_file(examples.get_path("crimes.shp"))
all_crimes.crs = "esri:102649"
all_crimes = all_crimes.to_crs("epsg:2762")
all_crimes.head()
[6]:
| POLYID2 | POLYID | geometry | |
|---|---|---|---|
| 0 | 1 | 1 | POINT (221868.432 266920.497) |
| 1 | 2 | 2 | POINT (220923.246 266933.298) |
| 2 | 3 | 3 | POINT (221709.326 266960.731) |
| 3 | 4 | 4 | POINT (221900.131 266962.255) |
| 4 | 5 | 5 | POINT (221750.169 266962.864) |
Detective Königsberg’s cases¶
[7]:
numpy.random.seed(1960)
koenigsberg_cases = 7 * 2
subset_idx = numpy.random.choice(all_crimes.index, koenigsberg_cases, replace=False)
crimes_scenes = all_crimes[all_crimes.index.isin(subset_idx)].copy()
crimes_scenes
[7]:
| POLYID2 | POLYID | geometry | |
|---|---|---|---|
| 5 | 6 | 6 | POINT (221652.328 266963.169) |
| 11 | 12 | 12 | POINT (220775.113 266968.350) |
| 48 | 49 | 49 | POINT (220962.565 267281.381) |
| 62 | 63 | 63 | POINT (220772.979 267387.147) |
| 88 | 89 | 89 | POINT (220797.363 267546.558) |
| 114 | 115 | 115 | POINT (221501.452 267698.654) |
| 120 | 121 | 121 | POINT (220474.580 267731.267) |
| 132 | 133 | 133 | POINT (221677.932 267762.053) |
| 169 | 170 | 170 | POINT (221154.590 267920.549) |
| 184 | 185 | 185 | POINT (221853.497 268049.786) |
| 211 | 212 | 212 | POINT (220775.723 268150.369) |
| 234 | 235 | 235 | POINT (220473.361 268198.223) |
| 269 | 270 | 270 | POINT (220515.423 268478.944) |
| 279 | 280 | 280 | POINT (222084.231 268591.723) |
Instantiate a network object¶
[8]:
ntw = spaghetti.Network(in_data=streets)
vertices, arcs = spaghetti.element_as_gdf(ntw, vertices=True, arcs=True)
vertices.head()
[8]:
| id | geometry | comp_label | |
|---|---|---|---|
| 0 | 0 | POINT (222007.131 267348.711) | 0 |
| 1 | 1 | POINT (222007.159 267317.431) | 0 |
| 2 | 2 | POINT (222006.951 267549.880) | 0 |
| 3 | 3 | POINT (221420.428 267804.889) | 0 |
| 4 | 4 | POINT (221411.402 267921.993) | 0 |
[9]:
arcs.head()
[9]:
| id | geometry | comp_label | |
|---|---|---|---|
| 0 | (0, 1) | LINESTRING (222007.131 267348.711, 222007.159 ... | 0 |
| 1 | (0, 2) | LINESTRING (222007.131 267348.711, 222006.951 ... | 0 |
| 2 | (1, 110) | LINESTRING (222007.159 267317.431, 222081.565 ... | 0 |
| 3 | (1, 127) | LINESTRING (222007.159 267317.431, 221805.991 ... | 0 |
| 4 | (1, 213) | LINESTRING (222007.159 267317.431, 222007.338 ... | 0 |
Plot¶
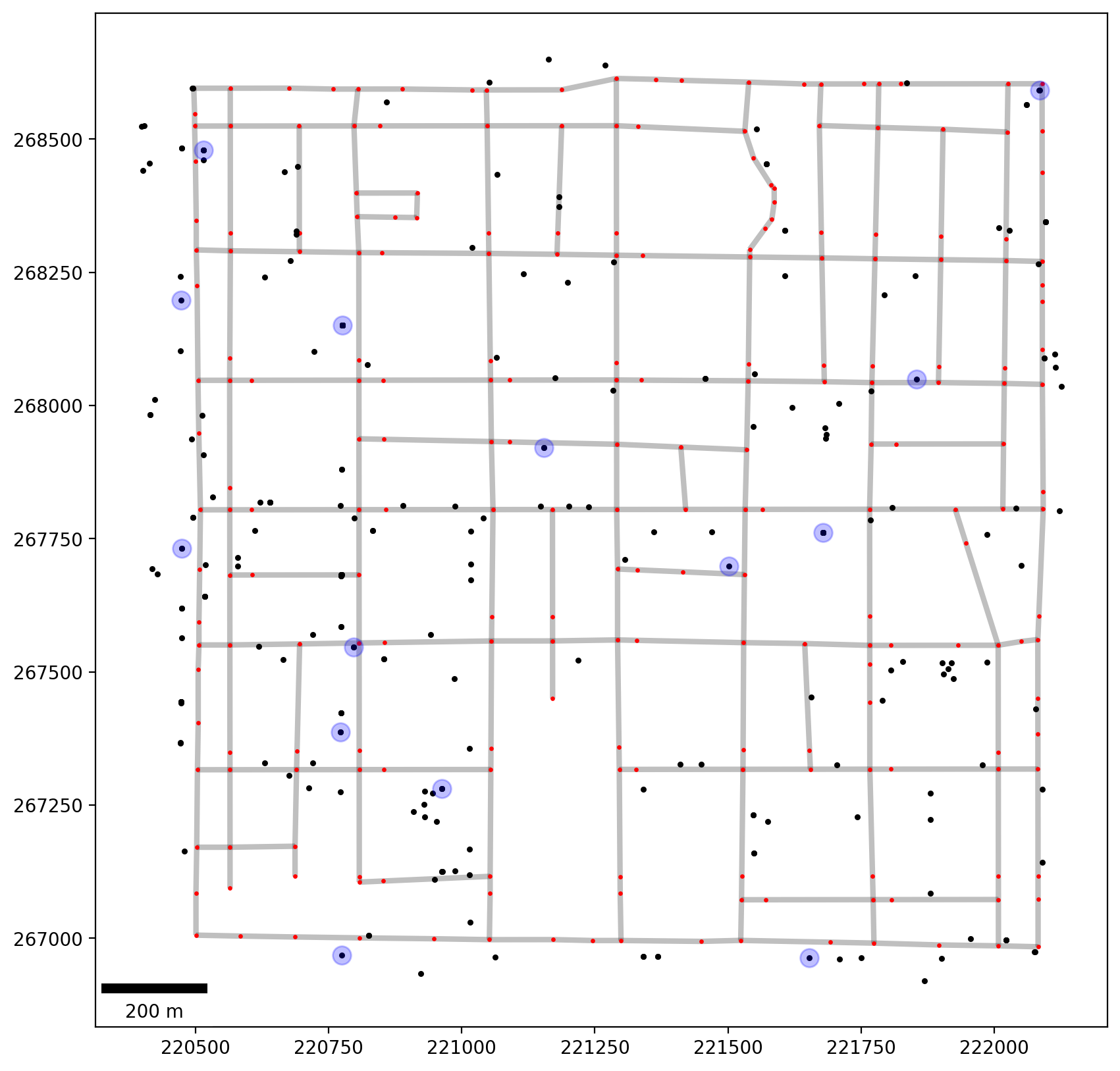
[10]:
base = arcs.plot(linewidth=3, alpha=0.25, color="k", zorder=0, figsize=(10, 10))
vertices.plot(ax=base, markersize=2, color="red", zorder=1)
all_crimes.plot(ax=base, markersize=5, color="k", zorder=2)
crimes_scenes.plot(ax=base, markersize=100, alpha=0.25, color="blue", zorder=2)
# add scale bar
scalebar = ScaleBar(1, units="m", location="lower left")
base.add_artist(scalebar);
Associate Detective Königsberg’s cases with the network and plot¶
[11]:
ntw.snapobservations(crimes_scenes, "crime_scenes")
pp_obs = spaghetti.element_as_gdf(ntw, pp_name="crime_scenes")
pp_obs_snapped = spaghetti.element_as_gdf(ntw, pp_name="crime_scenes", snapped=True)
pp_obs_snapped
[11]:
| id | geometry | comp_label | |
|---|---|---|---|
| 0 | 0 | POINT (221652.937 266993.226) | 0 |
| 1 | 1 | POINT (220775.569 267001.039) | 0 |
| 2 | 2 | POINT (220962.537 267316.554) | 0 |
| 3 | 3 | POINT (220807.668 267387.173) | 0 |
| 4 | 4 | POINT (220797.239 267554.033) | 0 |
| 5 | 5 | POINT (221500.788 267683.891) | 0 |
| 6 | 6 | POINT (220508.813 267730.837) | 0 |
| 7 | 7 | POINT (221677.895 267805.108) | 0 |
| 8 | 8 | POINT (221154.800 267930.187) | 0 |
| 9 | 9 | POINT (221853.503 268043.032) | 0 |
| 10 | 10 | POINT (220807.081 268150.393) | 0 |
| 11 | 11 | POINT (220503.712 268198.499) | 0 |
| 12 | 12 | POINT (220499.864 268478.580) | 0 |
| 13 | 13 | POINT (222089.345 268591.727) | 0 |
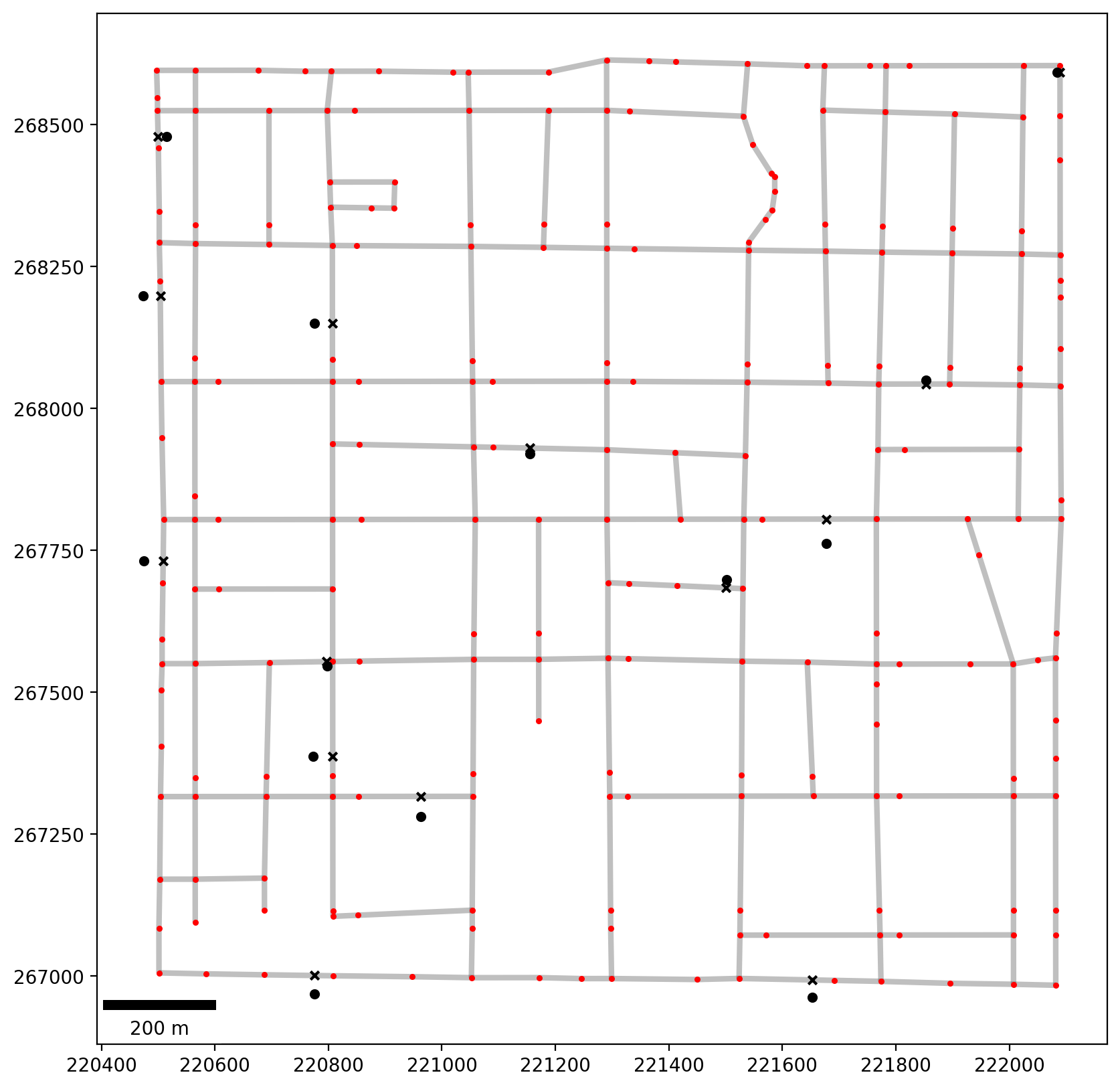
[12]:
base = arcs.plot(linewidth=3, alpha=0.25, color="k", zorder=0, figsize=(10, 10))
vertices.plot(ax=base, markersize=5, color="r", zorder=1)
pp_obs.plot(ax=base, markersize=20, color="k", zorder=2)
pp_obs_snapped.plot(ax=base, markersize=20, marker="x", color="k", zorder=2)
# add scale bar
scalebar = ScaleBar(1, units="m", location="lower left")
base.add_artist(scalebar);
Calculate distance matrix while generating shortest path trees¶
[13]:
d2d_dist, tree = ntw.allneighbordistances("crime_scenes", gen_tree=True)
d2d_dist[:3, :3]
[13]:
array([[ nan, 877.47303775, 1012.61325634],
[ 877.47303775, nan, 688.11683524],
[1012.61325634, 688.11683524, nan]])
[14]:
list(tree.items())[:4], list(tree.items())[-4:]
[14]:
([((0, 1), (164, 158)),
((0, 2), (164, 142)),
((0, 3), (164, 197)),
((0, 4), (164, 147))],
[((10, 13), (72, 98)),
((11, 12), (26, 29)),
((11, 13), (26, 85)),
((12, 13), (30, 85))])
3. The Travling Salesperson Problem¶
Create decision variables for the crime scene locations¶
[15]:
pp_obs["dv"] = pp_obs["id"].apply(lambda _id: "x_%s" % _id)
pp_obs
[15]:
| id | geometry | comp_label | dv | |
|---|---|---|---|---|
| 0 | 0 | POINT (221652.328 266963.169) | 0 | x_0 |
| 1 | 1 | POINT (220775.113 266968.350) | 0 | x_1 |
| 2 | 2 | POINT (220962.565 267281.381) | 0 | x_2 |
| 3 | 3 | POINT (220772.979 267387.147) | 0 | x_3 |
| 4 | 4 | POINT (220797.363 267546.558) | 0 | x_4 |
| 5 | 5 | POINT (221501.452 267698.654) | 0 | x_5 |
| 6 | 6 | POINT (220474.580 267731.267) | 0 | x_6 |
| 7 | 7 | POINT (221677.932 267762.053) | 0 | x_7 |
| 8 | 8 | POINT (221154.590 267920.549) | 0 | x_8 |
| 9 | 9 | POINT (221853.497 268049.786) | 0 | x_9 |
| 10 | 10 | POINT (220775.723 268150.369) | 0 | x_10 |
| 11 | 11 | POINT (220473.361 268198.223) | 0 | x_11 |
| 12 | 12 | POINT (220515.423 268478.944) | 0 | x_12 |
| 13 | 13 | POINT (222084.231 268591.723) | 0 | x_13 |
Solve the TSP¶
[16]:
mtz_tsp = MTZ_TSP(pp_obs["dv"], d2d_dist)
x_0,1: 1.0
x_1,2: 1.0
x_10,8: 1.0
x_11,12: 1.0
x_12,10: 1.0
x_13,7: 1.0
x_2,3: 1.0
x_3,4: 1.0
x_4,6: 1.0
x_5,0: 1.0
x_6,11: 1.0
x_7,5: 1.0
x_8,9: 1.0
x_9,13: 1.0
Status: Optimal
Extract all network shortest paths¶
[17]:
paths = ntw.shortest_paths(tree, "crime_scenes")
paths_gdf = spaghetti.element_as_gdf(ntw, routes=paths)
paths_gdf.head()
[17]:
| geometry | O | D | id | |
|---|---|---|---|---|
| 0 | LINESTRING (221652.937 266993.226, 221523.786 ... | 0 | 1 | (0, 1) |
| 1 | LINESTRING (221652.937 266993.226, 221523.786 ... | 0 | 2 | (0, 2) |
| 2 | LINESTRING (221652.937 266993.226, 221523.786 ... | 0 | 3 | (0, 3) |
| 3 | LINESTRING (221652.937 266993.226, 221523.786 ... | 0 | 4 | (0, 4) |
| 4 | LINESTRING (221652.937 266993.226, 221523.786 ... | 0 | 5 | (0, 5) |
Extract the tour¶
[18]:
tour = mtz_tsp.extract_tour(paths_gdf.copy(), "id")
tour.head()
[18]:
| geometry | O | D | id | leg | |
|---|---|---|---|---|---|
| 0 | LINESTRING (221652.937 266993.226, 221523.786 ... | 0 | 1 | (0, 1) | 0 |
| 13 | LINESTRING (220775.569 267001.039, 220807.966 ... | 1 | 2 | (1, 2) | 1 |
| 25 | LINESTRING (220962.537 267316.554, 220853.585 ... | 2 | 3 | (2, 3) | 2 |
| 36 | LINESTRING (220807.668 267387.173, 220807.540 ... | 3 | 4 | (3, 4) | 3 |
| 47 | LINESTRING (220797.239 267554.033, 220695.934 ... | 4 | 6 | (4, 6) | 4 |
Define label helper functions and plot Det. Königsberg’s optimal tour¶
[19]:
def tour_labels(t, b):
"""Label each leg of the tour."""
def _lab_loc(_x):
"""Helper for labeling location."""
return _x.geometry.interpolate(0.5, normalized=True).coords[0]
kws = {"size": 20, "ha": "center", "va": "bottom", "weight": "bold"}
t.apply(lambda x: b.annotate(text=x.leg, xy=_lab_loc(x), **kws), axis=1)
def obs_labels(o, b):
"""Label each point pattern observation."""
def _lab_loc(_x):
"""Helper for labeling observations."""
return _x.geometry.coords[0]
kws = {"size": 14, "ha": "left", "va": "bottom", "style": "oblique", "color": "k"}
o.apply(lambda x: b.annotate(text=x.id, xy=_lab_loc(x), **kws), axis=1)
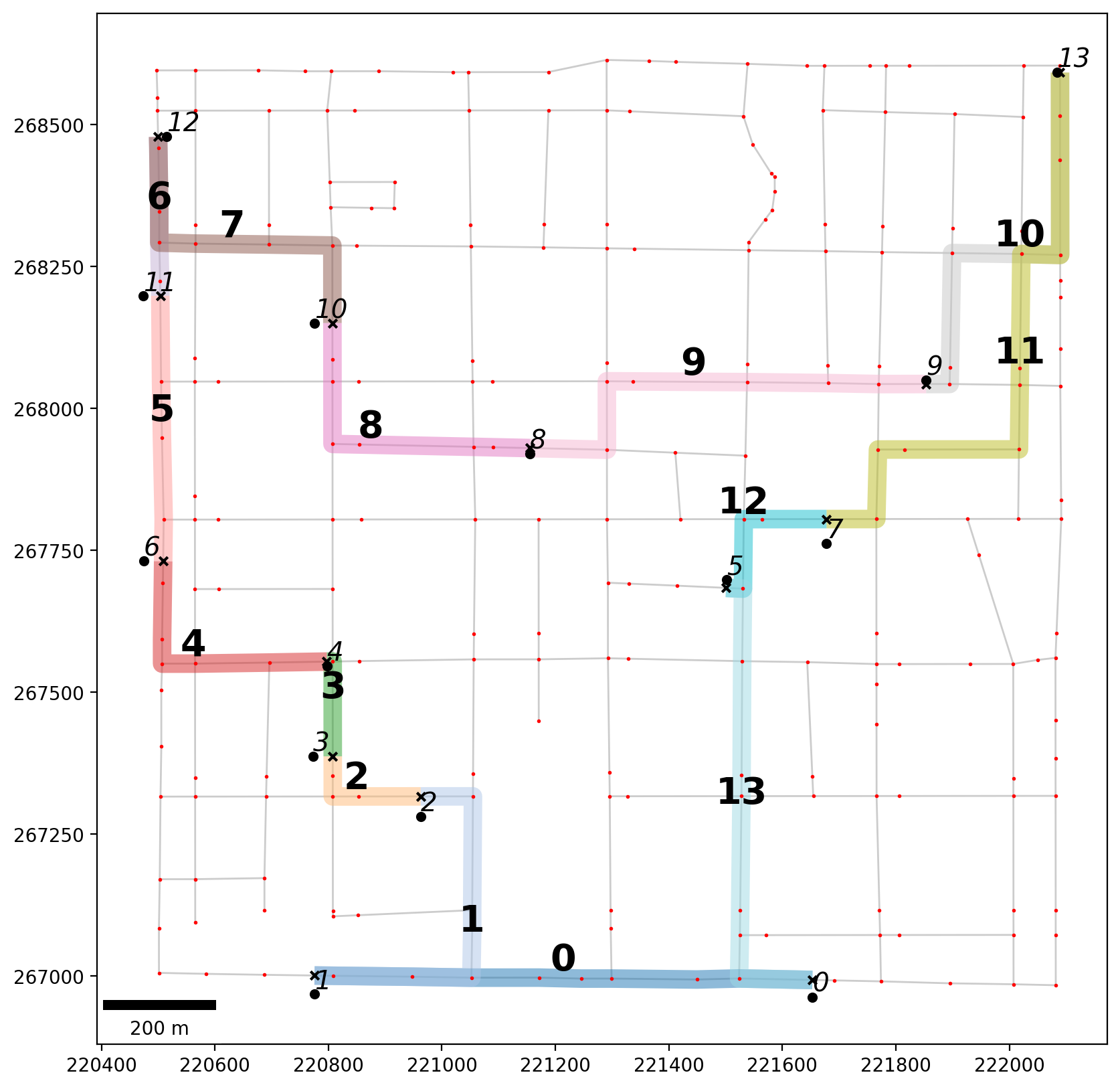
[20]:
base = arcs.plot(alpha=0.2, linewidth=1, color="k", figsize=(10, 10), zorder=0)
tour.plot(ax=base, column="leg", cmap="tab20", alpha=0.50, linewidth=10, zorder=1)
vertices.plot(ax=base, markersize=1, color="r", zorder=2)
pp_obs.plot(ax=base, markersize=20, color="k", zorder=3)
pp_obs_snapped.plot(ax=base, markersize=20, color="k", marker="x", zorder=2)
# tour leg labels
tour_labels(tour, base)
# crime scene labels
obs_labels(pp_obs, base)
# add scale bar
scalebar = ScaleBar(1, units="m", location="lower left")
base.add_artist(scalebar);