This page was generated from notebooks/network-spatial-weights.ipynb. Interactive online version: Binder badge

If any part of this notebook is used in your research, please cite with the reference found in README.md.

Network spatial weights

Plotting demonstration of network arc contiguity in spaghetti

Author: James D. Gaboardi jgaboardi@gmail.com

This notebook demonstrates plotting for the following:

  1. A basic geometric object (triangle) represented as a network

  2. A regular lattice

  3. An empirical example

[1]:

%config InlineBackend.figure_format = "retina"

[2]:

%load_ext watermark
%watermark

Last updated: 2022-11-01T23:12:56.027784-04:00

Python implementation: CPython
Python version       : 3.10.6
IPython version      : 8.6.0

Compiler    : Clang 13.0.1
OS          : Darwin
Release     : 22.1.0
Machine     : x86_64
Processor   : i386
CPU cores   : 8
Architecture: 64bit


[3]:

import geopandas
import libpysal
from libpysal.cg import Point, Chain
import matplotlib
import matplotlib.pyplot as plt
import spaghetti
%matplotlib inline
%watermark -w
%watermark -iv

Watermark: 2.3.1

spaghetti : 1.6.8
libpysal  : 4.6.2
matplotlib: 3.6.1
json      : 2.0.9
geopandas : 0.12.1


/Users/the-gaboardi/miniconda3/envs/py310_spgh_dev/lib/python3.10/site-packages/spaghetti/network.py:39: FutureWarning: The next major release of pysal/spaghetti (2.0.0) will drop support for all ``libpysal.cg`` geometries. This change is a first step in refactoring ``spaghetti`` that is expected to result in dramatically reduced runtimes for network instantiation and operations. Users currently requiring network and point pattern input as ``libpysal.cg`` geometries should prepare for this simply by converting to ``shapely`` geometries.
  warnings.warn(f"{dep_msg}", FutureWarning)

Helper function for plotting weights

[4]:

def plot_weights(_ntw, _arcs_df, _base):
    """Plot network arc spatial weights."""
    node_kws, edge_kws = {"s":100, "zorder":2}, {"zorder":1}
    w_kws = {"edge_kws":edge_kws, "node_kws":node_kws}
    _ntw.w_network.plot(_arcs_df, indexed_on="id", ax=_base, **w_kws)

Helper functions for arc and vertex labeling

[5]:

def arc_labels(a, b, s, offset=[0.035, 0.0]):
    """Label each network arc."""
    def _lab_loc(_x):
        """Helper for labeling network arcs."""
        xy = _x.geometry.interpolate(0.5, normalized=True).coords[0]
        xy = tuple([_xy+o for (_xy,o) in zip(xy,offset)])
        return xy
    kws = {"ha":"left", "va":"bottom","weight":"bold","color":"k","size":s}
    a.apply(lambda x: b.annotate(text=x.id, xy=_lab_loc(x), **kws), axis=1)

def vert_labels(v, b, s, offset=[0.025, 0.025]):
    """Label each network vertex."""
    def _lab_loc(_x):
        """Internal helper for labeling vertices."""
        xy = _x.geometry.coords[0]
        xy = tuple([_xy+o for (_xy,o) in zip(xy,offset)])
        return xy
    kws = {"ha":"left", "va":"bottom","weight":"bold","color":"r","size":s}
    v.apply(lambda x: b.annotate(text=x.id, xy=_lab_loc(x), **kws), axis=1)

1. Triangle

Generate a spaghetti.Network and plot

[6]:

triangle = [
    Chain([Point([0, 0]), Point([0, 3])]),
    Chain([Point([0, 3]), Point([4, 0])]),
    Chain([Point([4, 0]), Point([0, 0])]),
]
triangle

[6]:

[<libpysal.cg.shapes.Chain at 0x1674c5510>,
 <libpysal.cg.shapes.Chain at 0x1674c5bd0>,
 <libpysal.cg.shapes.Chain at 0x1674c5a80>]

[7]:

ntw = spaghetti.Network(in_data=triangle)
vertices_df, arcs_df = spaghetti.element_as_gdf(ntw, vertices=True, arcs=True)

[8]:

base_kws = {"figsize":(12, 12), "lw":5, "color":"k", "zorder":0}
base = arcs_df.plot(**base_kws, alpha=.35)
vertices_df.plot(ax=base, fc="r", ec="k", markersize=50, zorder=2)
# arc labels
arc_labels(arcs_df, base, 12)
# vertex labels
vert_labels(vertices_df, base, 14)
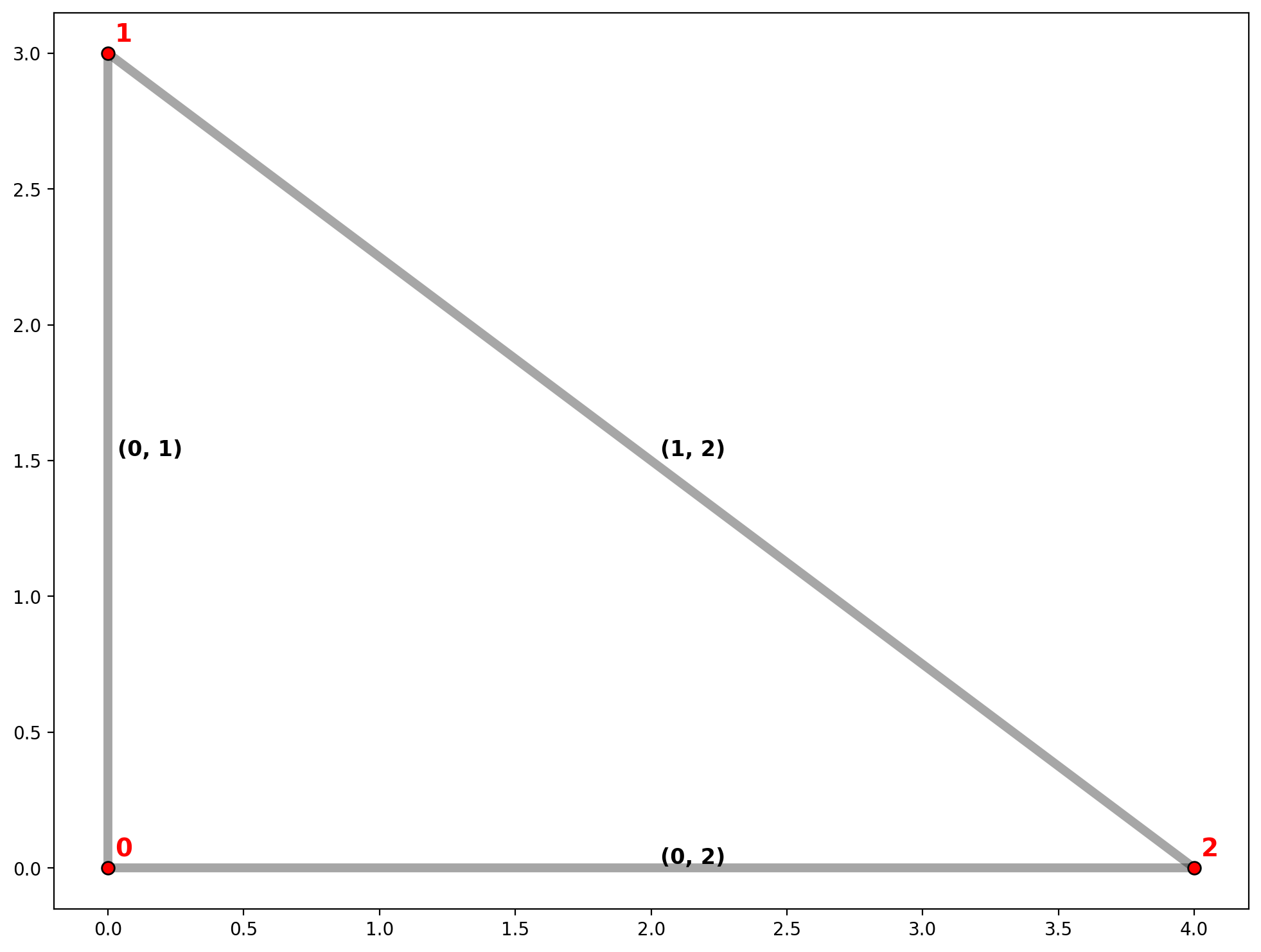
../_images/notebooks_network-spatial-weights_11_0.png

An arc-based spatial weights attribute is generated with network instantiaton—w_network.

[9]:

ntw.w_network

[9]:

<libpysal.weights.weights.W at 0x1674c5ea0>

[10]:

print(dir(ntw.w_network))

['_W__get_id_order', '_W__neighbors_0', '_W__set_id_order', '__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__getitem__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__iter__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', '_build_sparse', '_cache', '_cardinalities', '_component_labels', '_id2i', '_id_order', '_id_order_set', '_n', '_n_components', '_reset', '_sparse', '_transform', 'asymmetries', 'asymmetry', 'cardinalities', 'component_labels', 'diagW2', 'diagWtW', 'diagWtW_WW', 'from_WSP', 'from_adjlist', 'from_file', 'from_networkx', 'from_shapefile', 'full', 'get_transform', 'histogram', 'id2i', 'id_order', 'id_order_set', 'islands', 'max_neighbors', 'mean_neighbors', 'min_neighbors', 'n', 'n_components', 'neighbor_offsets', 'neighbors', 'nonzero', 'pct_nonzero', 'plot', 'remap_ids', 's0', 's1', 's2', 's2array', 'sd', 'set_shapefile', 'set_transform', 'silence_warnings', 'sparse', 'symmetrize', 'to_WSP', 'to_adjlist', 'to_file', 'to_networkx', 'transform', 'transformations', 'trcW2', 'trcWtW', 'trcWtW_WW', 'weights']

The plot() method in the libpysal.weights.W class can be used along with a geopandas.GeoDataFrame to visualize contiguity.

[11]:

base = arcs_df.plot(**base_kws, alpha=.35)
plot_weights(ntw, arcs_df, base)
vertices_df.plot(ax=base, fc="r", ec="k", markersize=50, zorder=2)
# arc labels
arc_labels(arcs_df, base, 12)
# vertex labels
vert_labels(vertices_df, base, 14)
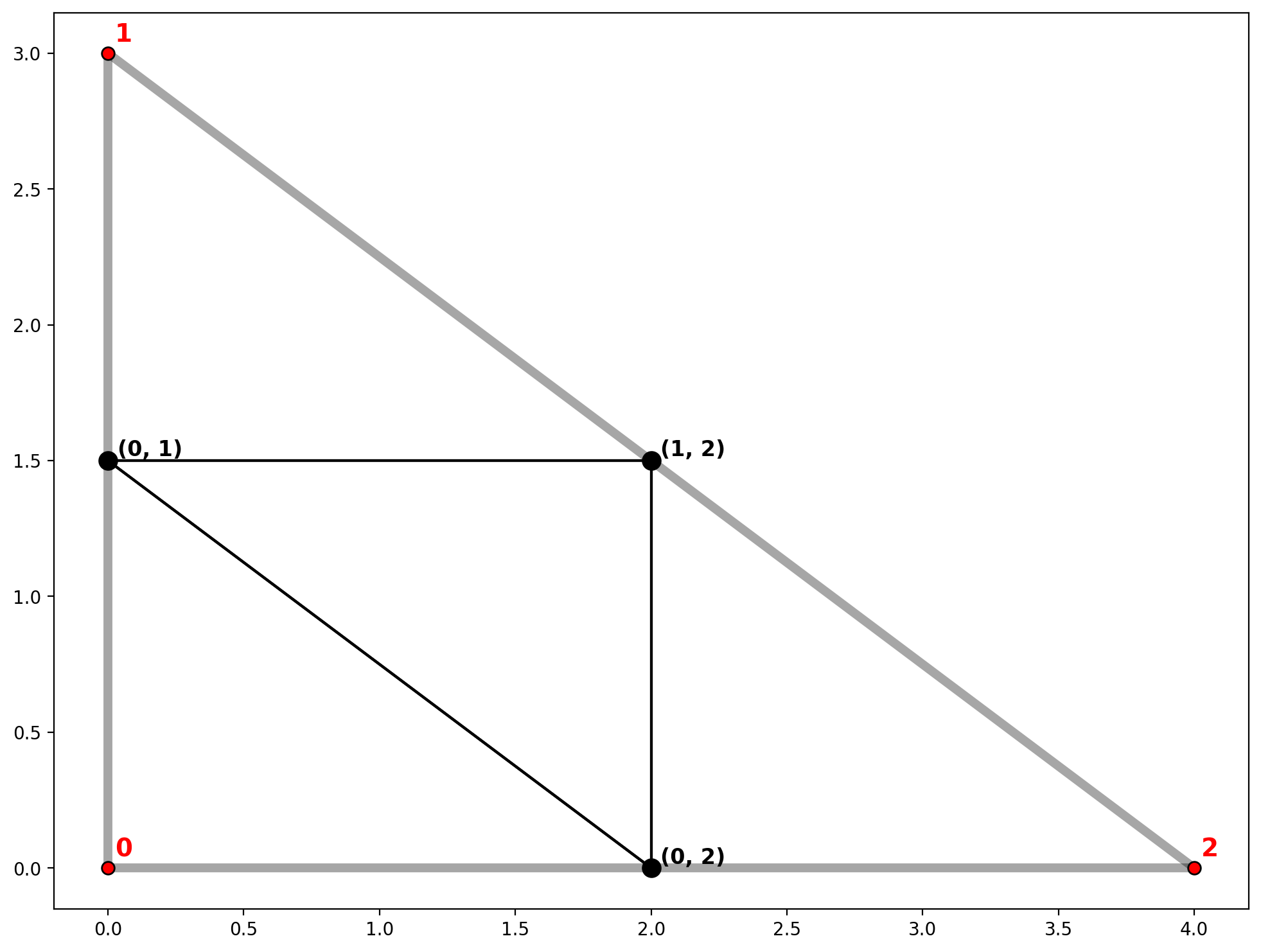
../_images/notebooks_network-spatial-weights_16_0.png

2. Regular lattice

Generate a spaghetti.Network from a 4x4 regular lattice and plot

[12]:

lattice = spaghetti.regular_lattice((0,0,3,3), 2, exterior=True)
ntw = spaghetti.Network(in_data=lattice)

[13]:

vertices_df, arcs_df = spaghetti.element_as_gdf(ntw, vertices=True, arcs=True)

[14]:

base = arcs_df.plot(**base_kws, alpha=.35)
plot_weights(ntw, arcs_df, base)
vertices_df.plot(ax=base, fc="r", ec="k", markersize=50, zorder=2)
# arc labels
arc_labels(arcs_df, base, 12)
# vertex labels
vert_labels(vertices_df, base, 14)
plt.xlim(-0.25, 3.5);
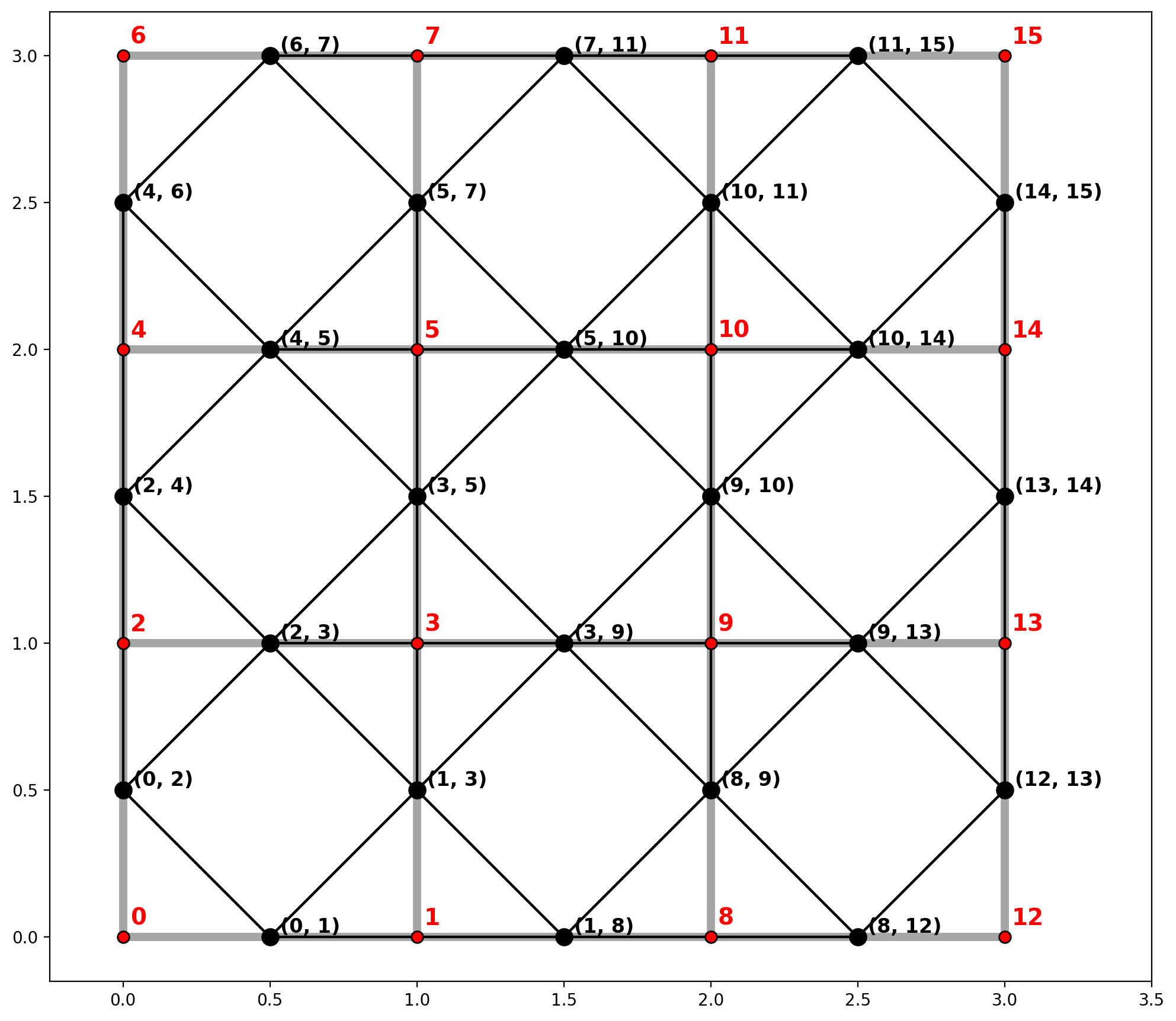
../_images/notebooks_network-spatial-weights_20_0.png

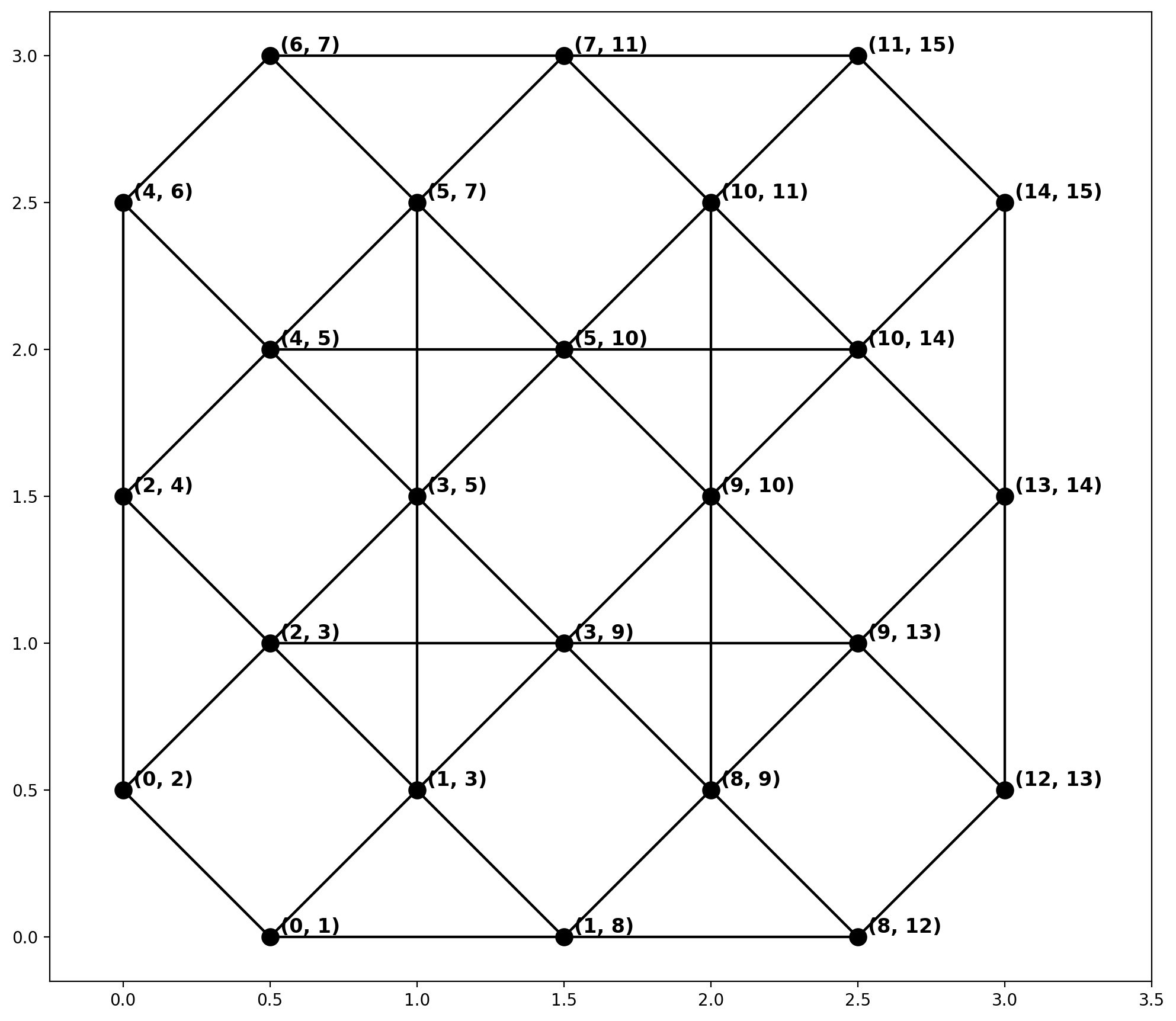
Plot only the arc weights

[15]:

base = arcs_df.plot(**base_kws, alpha=.0)
plot_weights(ntw, arcs_df, base)
arc_labels(arcs_df, base, 12)
plt.xlim(-0.25, 3.5);
../_images/notebooks_network-spatial-weights_22_0.png

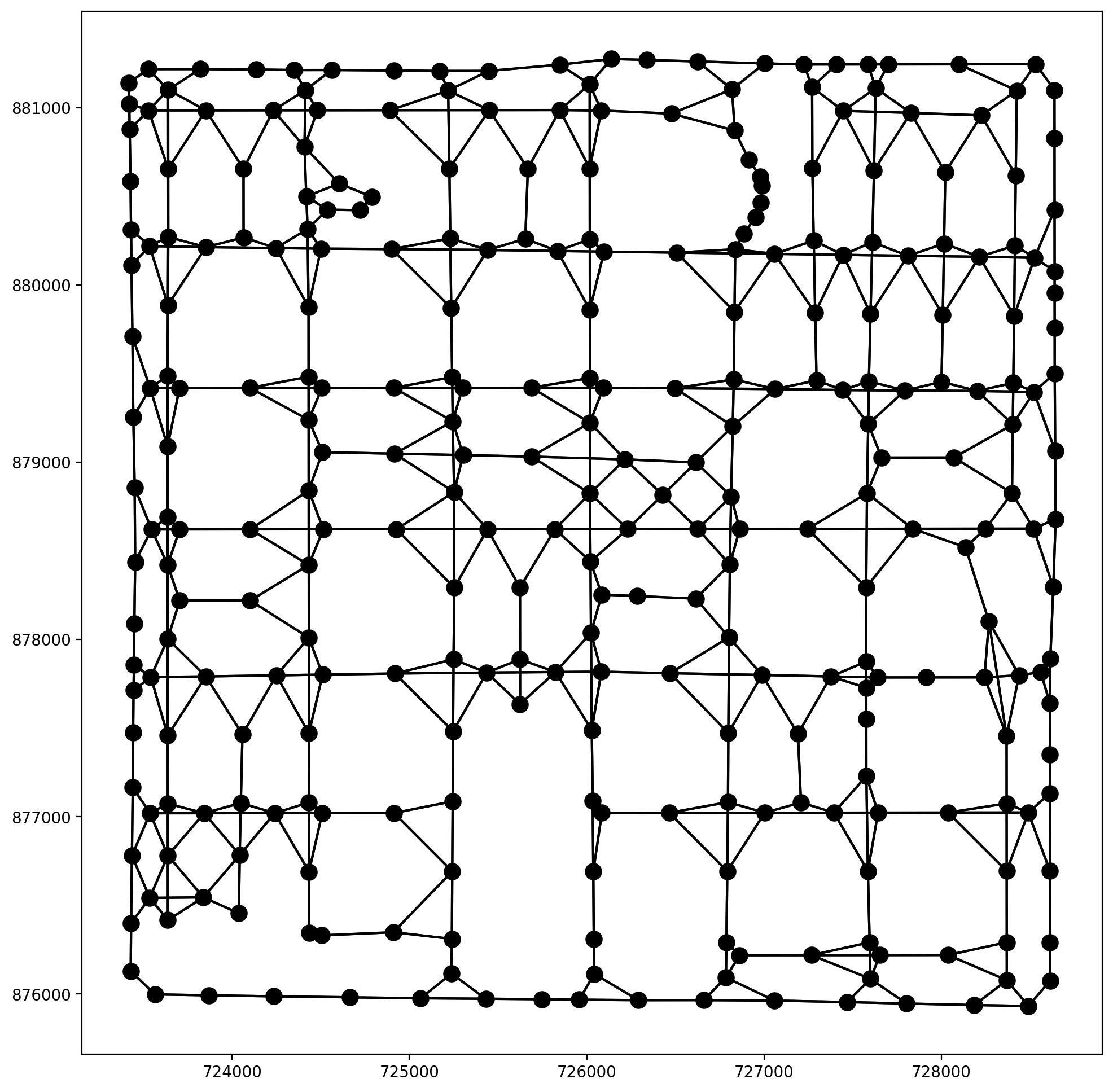
3. Emprical Example — geodanet/streets.shp

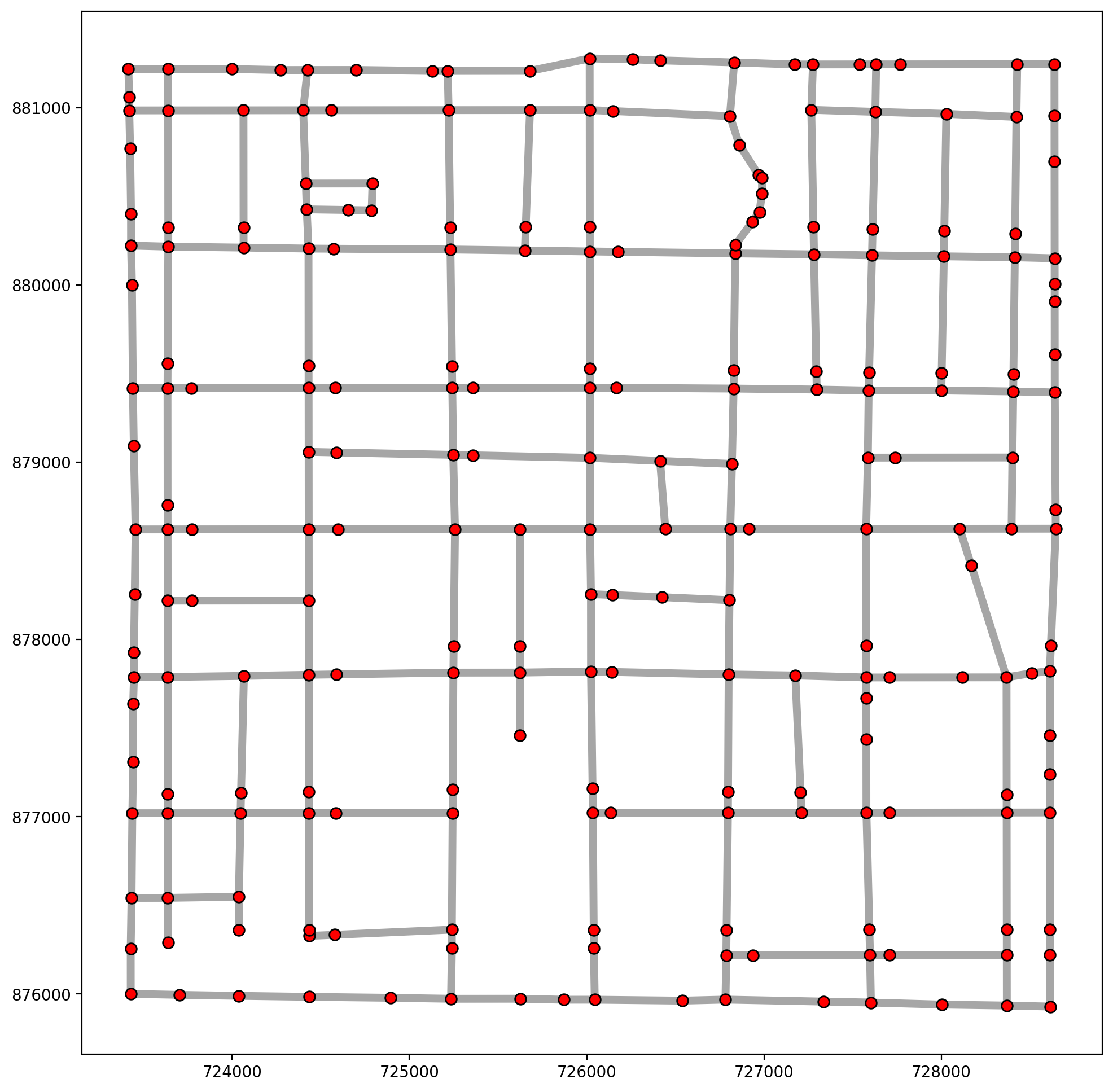
Read in a libpysal.example and create a spaghetti.Network, then plot.

[16]:

ntw = spaghetti.Network(in_data=libpysal.examples.get_path("streets.shp"))

[17]:

vertices_df, arcs_df = spaghetti.element_as_gdf(ntw, vertices=True, arcs=True)

[18]:

base = arcs_df.plot(**base_kws, alpha=.35)
vertices_df.plot(ax=base, fc="r", ec="k", markersize=50, zorder=2);
../_images/notebooks_network-spatial-weights_26_0.png 
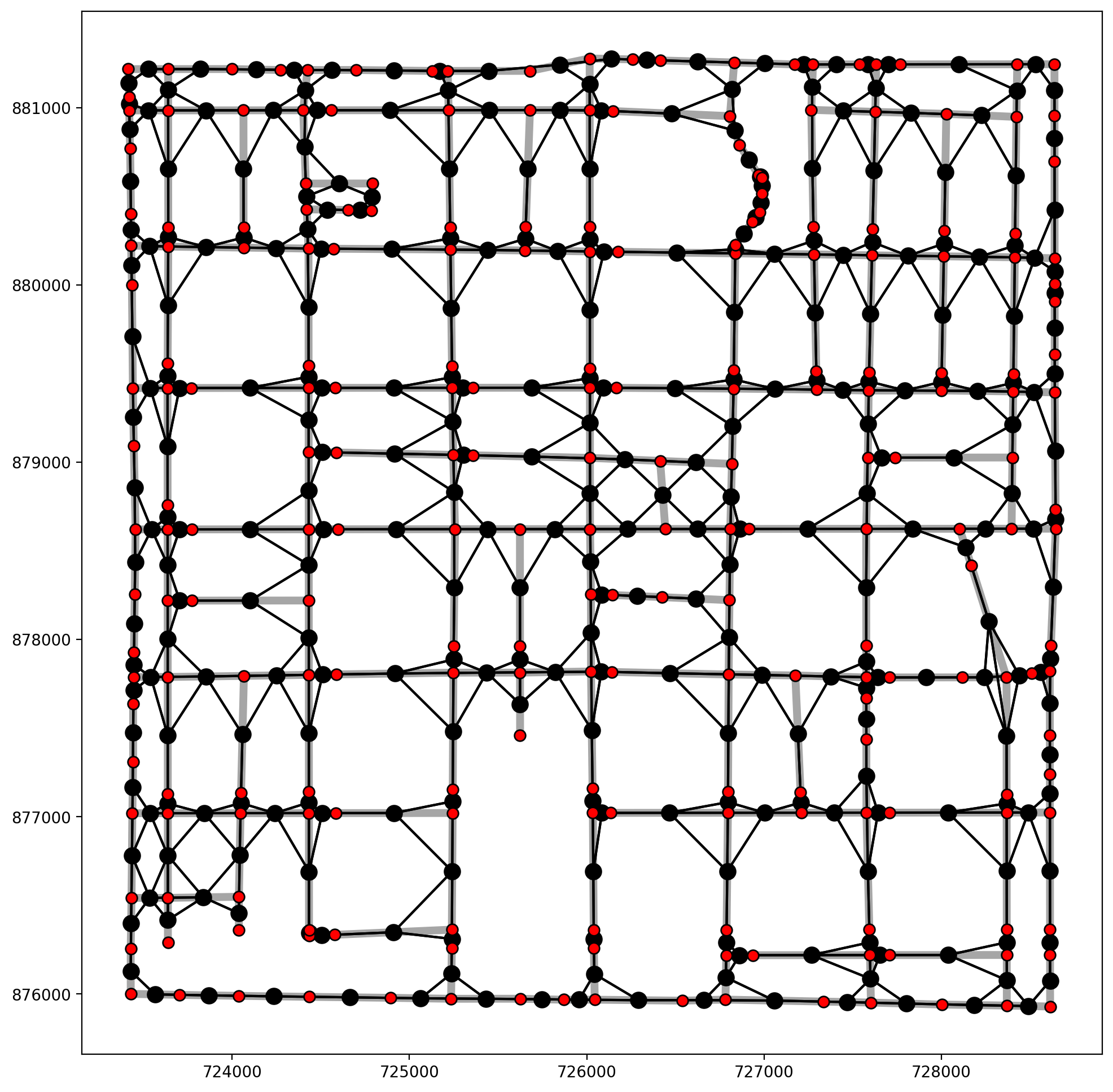
[19]:

base = arcs_df.plot(**base_kws, alpha=.35)
plot_weights(ntw, arcs_df, base)
vertices_df.plot(ax=base, fc="r", ec="k", markersize=50, zorder=2);
../_images/notebooks_network-spatial-weights_27_0.png 
[20]:

base = arcs_df.plot(**base_kws, alpha=.0)
plot_weights(ntw, arcs_df, base)
../_images/notebooks_network-spatial-weights_28_0.png