This page was generated from /home/runner/work/esda/esda/docs/notebooks/adbscan_berlin_example.ipynb. Interactive online version:

Cluster points and explore boundary blurriness with A-DBSCAN

In this example, we will illustrate how to use A-DBSCAN (Arribas-Bel et al., 2019) with a sample of AirBnb properties in Berlin. A-DBSCAN will allow us do two things:

• Identify clusters of high density of AirBnb properties and delineate their boundaries

• Explore the stability of such boundaries

%matplotlib inline

import pandas
import geopandas
import numpy as np
import contextily as cx
import matplotlib.pyplot as plt
from shapely.geometry import Polygon
from libpysal.cg.alpha_shapes import alpha_shape_auto

import sys
sys.path.append("../")
try:
    from esda.adbscan import ADBSCAN, get_cluster_boundary, remap_lbls
# This below can be removed once A-DBSCAN is merged into `esda`
except:
    print("Import from local folder...")
    import sys
    sys.path.append("../esda")
    from adbscan import ADBSCAN, get_cluster_boundary, remap_lbls

Data

We will be using the Berlin extract from Inside Airbnb. This is the same dataset used in the Scipy 2018 tutorial on Geospatial data analysis with Python.

tab = pandas.read_csv("data/berlin-listings.csv")
tab.head(2)

	Unnamed: 0	id	listing_url	scrape_id	last_scraped	name	summary	space	description	experiences_offered	...	review_scores_value	requires_license	license	jurisdiction_names	instant_bookable	cancellation_policy	require_guest_profile_picture	require_guest_phone_verification	calculated_host_listings_count	reviews_per_month
0	0	17260587	https://www.airbnb.com/rooms/17260587	20170507222235	2017-05-08	Kunterbuntes Zimmer mit eigenem Bad für jedermann	Meine Unterkunft ist gut für paare, alleinreis...	NaN	Meine Unterkunft ist gut für paare, alleinreis...	none	...	10.0	f	NaN	NaN	t	flexible	f	f	3	2.00
1	1	17227881	https://www.airbnb.com/rooms/17227881	20170507222235	2017-05-08	Modernes Zimmer in Berlin Pankow	Es ist ein schönes gepflegtes und modernes Zim...	Das Haus befindet sich direkt vor eine Tram Ha...	Es ist ein schönes gepflegtes und modernes Zim...	none	...	10.0	f	NaN	NaN	t	flexible	f	f	1	1.29

2 rows × 96 columns

The original dataset includes more than 20,000 observations:

tab.shape

(20053, 96)

To make the illustration run a bit speedier on any hardware, let us pick a random sample of 10% of the set; that is we’ll pick 2,000 properties at random:

tab = tab.sample(n=2000, random_state=1234)

For convenience, we convert into a GeoDataFrame where the geometries are built from the lon/lat columns in the original table:

db_ll = geopandas.GeoDataFrame(tab,
                               geometry=geopandas.points_from_xy(tab.longitude, tab.latitude),
                               crs={'init': 'epsg:4326'}
                              )

/home/serge/anaconda3/envs/analytical/lib/python3.7/site-packages/pyproj/crs/crs.py:53: FutureWarning: '+init=<authority>:<code>' syntax is deprecated. '<authority>:<code>' is the preferred initialization method. When making the change, be mindful of axis order changes: https://pyproj4.github.io/pyproj/stable/gotchas.html#axis-order-changes-in-proj-6
  return _prepare_from_string(" ".join(pjargs))

Because we are going to run an algorithm that relies on distances, we need to be able to calculate such distances in a projected plane. Instead of the original lon/lat coordinates, we use the `ETRS89 <http://epsg.io/5243>`__ projection, designed for Germany and expressed in metres:

db = db_ll.to_crs(epsg=5243)

Voila! We can now visualise our dataset:

ax = db.plot(markersize=0.1, color='orange')
cx.add_basemap(ax, crs=db.crs.to_string());

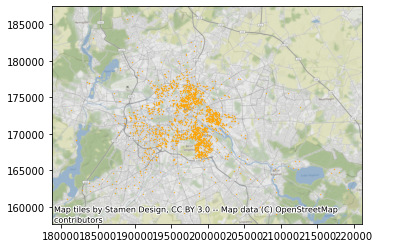
And before we get going, we will also pull out the projected coordinates into separate columns:

db["X"] = db.geometry.x
db["Y"] = db.geometry.y

Identify clusters of AirBnb

A-DBSCAN, similar to the original DBSCAN algorithm, requires two parameters before it can be run:

1. eps: maximum distance to look for neighbors from each location

2. min_samples: minimum number of neighboring points required for a point to be considered part of a cluster

For this example, we will pick a 1% of the overall sample size for the min_samples parameter:

db.shape[0] * 0.01

20.0

We will use a maximum radious of 500m for the eps parameter. This implicitly implies we are looking at a density of at least about 25 properties per Sq. \(Km^2\) (\(dens = \frac{20}{\pi \, \times \, 0.5^2}\)).

Once we know the parameters we’ll use, we can go ahead and run A-DBSCAN:

%%time
# Get clusters
adbs = ADBSCAN(500, 20, pct_exact=0.5, reps=10, keep_solus=True)
np.random.seed(1234)
adbs.fit(db)

CPU times: user 755 ms, sys: 3.36 ms, total: 758 ms
Wall time: 752 ms

ADBSCAN(eps=500, keep_solus=True, min_samples=20, pct_exact=0.5, reps=10)

Once fit(), we can extract the labels in a similar way that we would from scikit-learn, and then we can plot on a map:

ax = db.assign(lbls=adbs.votes["lbls"])\
       .plot(column="lbls",
             categorical=True,
             markersize=2.5,
             figsize=(12, 12)
            )
cx.add_basemap(ax, crs=db.crs.to_string());

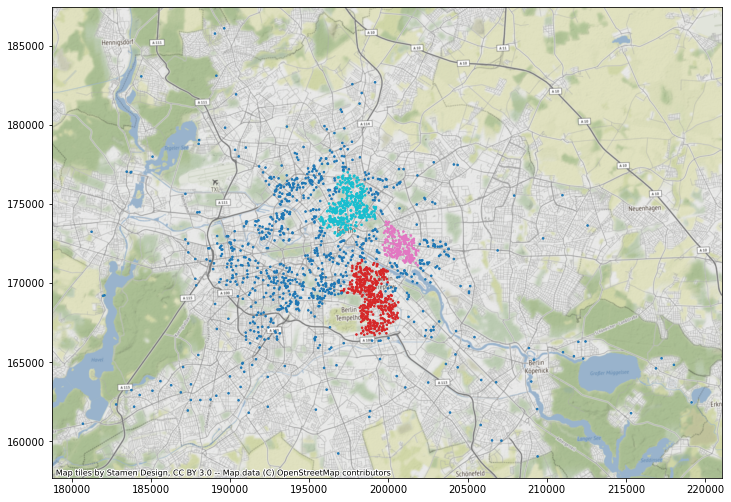
This only displays each property colored based on its label assigned. Beyond this, we can also create polygons that represent a tight boundary around all the points in a given cluster. To do this, we use the \(\alpha\)-shapes algorithm through the helper function get_cluster_boundary:

%time polys = get_cluster_boundary(adbs.votes["lbls"], db, crs=db.crs)

CPU times: user 1.76 s, sys: 15.2 ms, total: 1.78 s
Wall time: 1.77 s

These polygons can also be plotted as any other GeoSeries object:

ax = polys.plot(alpha=0.5, color="red")
cx.add_basemap(ax, crs=polys.crs.to_string());

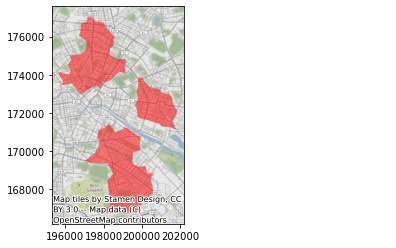
And, just for fun, we can create more zoomed-in views, dimming out areas outside each cluster:

f, axs = plt.subplots(1, 3, figsize=(18, 6))
for i, ax in enumerate(axs):
    # Plot the boundary of the cluster found
    ax = polys[[i]].plot(ax=ax,
                         edgecolor="red",
                         facecolor="none"
                        )
    # Add basemap
    cx.add_basemap(ax,
                   crs=polys.crs.to_string(),
                   url=cx.providers.CartoDB.Voyager,
                   zoom=13
                  )
    # Extra to dim non-cluster areas
    (minX, maxX), (minY, maxY) = ax.get_xlim(), ax.get_ylim()
    bb = Polygon([(minX, minY),
                  (maxX, minY),
                  (maxX, maxY),
                  (minX, maxY),
                  (minX, minY)
                 ])
    geopandas.GeoSeries([bb.difference(polys[i])],
                        crs=polys.crs
                       ).plot(ax=ax,
                              color='k',
                              alpha=0.5
                             )
    ax.set_axis_off()
    ax.set_title(f"Cluster {polys[[i]].index[0]}")
plt.show()

/home/serge/anaconda3/envs/analytical/lib/python3.7/site-packages/ipykernel_launcher.py:12: FutureWarning: The "url" option is deprecated. Please use the "source" argument instead.
  if sys.path[0] == '':
/home/serge/anaconda3/envs/analytical/lib/python3.7/site-packages/ipykernel_launcher.py:12: FutureWarning: The "url" option is deprecated. Please use the "source" argument instead.
  if sys.path[0] == '':
/home/serge/anaconda3/envs/analytical/lib/python3.7/site-packages/ipykernel_launcher.py:12: FutureWarning: The "url" option is deprecated. Please use the "source" argument instead.
  if sys.path[0] == '':

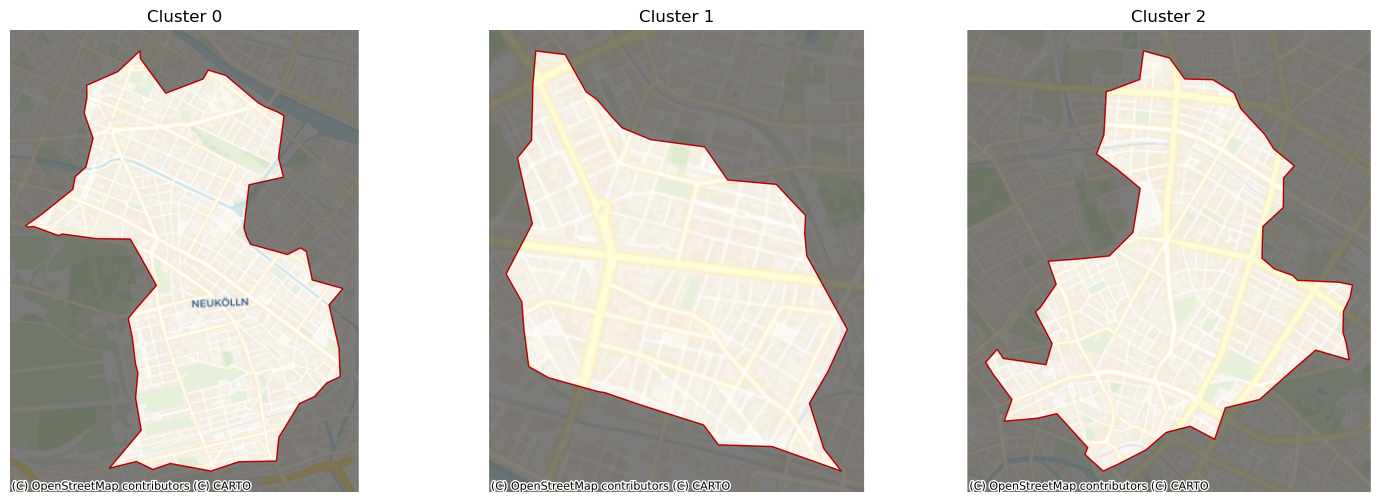
Explore boundary blurriness

One of the key benefits of A-DBSCAN is that, because it relies on an ensemble approach that generates several candidate solutions, it allows us to explore to what extent boundaries are stable and clearcut or blurrier. To do this, we need to extract from the ADBSCAN object each candidate solution and turn them into boundary lines (this may take a little bit to run):

%%time
solus_rl = remap_lbls(adbs.solus, db, n_jobs=-1)
lines = []
for rep in solus_rl:
    line = get_cluster_boundary(solus_rl[rep],
                                db,
                                crs=db.crs,
                                n_jobs=-1
                               )
    line = line.boundary
    line = line.reset_index()\
               .rename(columns={0: "geometry",
                                "index": "cluster_id"}
                      )\
               .assign(rep=rep)
    lines.append(line)
lines = pandas.concat(lines)
lines = geopandas.GeoDataFrame(lines, crs=db.crs)

CPU times: user 665 ms, sys: 1.45 s, total: 2.12 s
Wall time: 4.83 s

Here is a first look at all the solutions drawn up from the simulation:

ax = lines.plot(color="#FFDB58",
                linewidth=0.5
               )
cx.add_basemap(ax,
               alpha=0.5,
               url=cx.providers.Stamen.TonerHybrid,
               crs=lines.crs.to_string()
              )

/home/serge/anaconda3/envs/analytical/lib/python3.7/site-packages/ipykernel_launcher.py:7: FutureWarning: The "url" option is deprecated. Please use the "source" argument instead.
  import sys

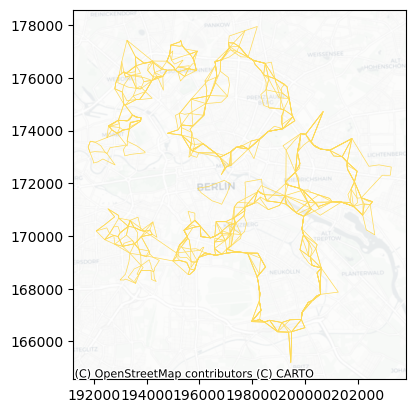
Having every single candidate boundary stored and labelled into a table, it allows us to make several queries. For example, here are all the solutions generated in the first replication:

lines.query("rep == 'rep-00'").plot()

<matplotlib.axes._subplots.AxesSubplot at 0x7fc0003522d0>

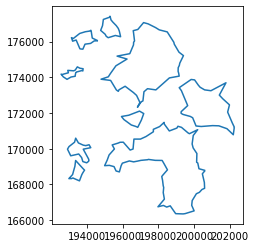
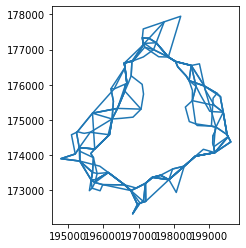
And here we have all the candidate solutions for cluster label No. 2:

lines.query("cluster_id == '2'").plot()

<matplotlib.axes._subplots.AxesSubplot at 0x7fc000452e90>

Finally, we can take this idea into an interactive context by building widgets that allow us to brush through replications:

from ipywidgets import interact, IntSlider

def plot_rep(rep):
    f, ax = plt.subplots(1, figsize=(9, 9))
    ax.set_facecolor("k")
    # Background points
    db[["X", "Y"]].plot.scatter("X", "Y", ax=ax, color="0.25", s=0.5)
    # Boundaries
    cs = lines.query(f"rep == 'rep-{str(rep).zfill(2)}'")
    cs.plot(ax=ax, color="red")
    # Cluster IDs
    for s, row in cs.iterrows():
        ax.text(row.geometry.centroid.x,
                row.geometry.centroid.y,
                s,
                size=20,
                c="w"
               )
    return None
reps = range(len(lines["rep"].unique()))
slider = IntSlider(min=min(reps), max=max(reps), step=1)
interact(plot_rep, rep=slider);

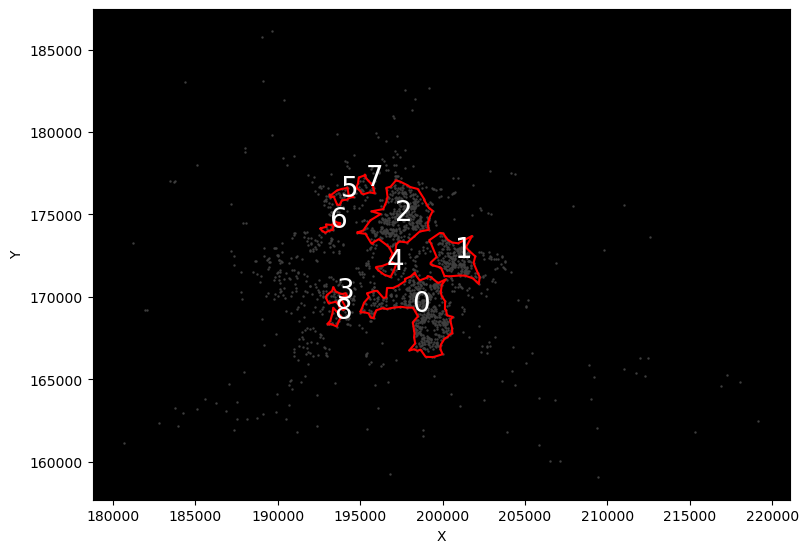
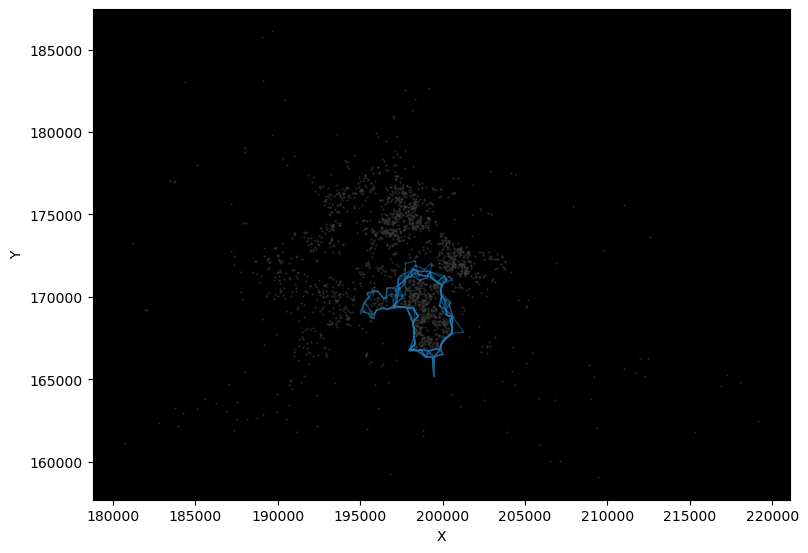
Or to pull out all solutions for a given cluster IDs:

def plot_cluster(cluster_id):
    f, ax = plt.subplots(1, figsize=(9, 9))
    ax.set_facecolor("k")
    # Background points
    db[["X", "Y"]].plot.scatter("X",
                                "Y",
                                ax=ax,
                                color="0.25",
                                s=0.5,
                                alpha=0.5
                               )
    # Boundaries
    lines.query(f"cluster_id == '{cluster_id}'").plot(ax=ax,
                                                      linewidth=1,
                                                      alpha=0.5
                                                     )
    return None
interact(plot_cluster, cluster_id=lines["cluster_id"].unique());