This page was generated from user-guide/weights/weights.ipynb. Interactive online version: Binder badge

Spatial Weights

[1]:

import sys
import os

[2]:

sys.path.append(os.path.abspath('..'))
import libpysal

[3]:

libpysal.examples.available()

[3]:

['georgia',
 '__pycache__',
 'tests',
 'newHaven',
 'Polygon_Holes',
 'nat',
 'Polygon',
 '10740',
 'berlin',
 'rio_grande_do_sul',
 'sids2',
 'sacramento2',
 'burkitt',
 'arcgis',
 'calemp',
 'stl',
 'virginia',
 'geodanet',
 'desmith',
 'book',
 'nyc_bikes',
 'Line',
 'south',
 'snow_maps',
 'Point',
 'street_net_pts',
 'guerry',
 '__pycache__',
 'baltim',
 'networks',
 'us_income',
 'taz',
 'columbus',
 'tokyo',
 'mexico',
 '__pycache__',
 'chicago',
 'wmat',
 'juvenile',
 'clearwater']

[4]:

libpysal.examples.explain('mexico')

[4]:

{'name': 'mexico',
 'description': 'Decennial per capita incomes of Mexican states 1940-2000',
 'explanation': ['* mexico.csv: attribute data. (n=32, k=13)',
  '* mexico.gal: spatial weights in GAL format.',
  '* mexicojoin.shp: Polygon shapefile. (n=32)',
  'Data used in Rey, S.J. and M.L. Sastre Gutierrez. (2010) "Interregional inequality dynamics in Mexico." Spatial Economic Analysis, 5: 277-298.']}

Weights from GeoDataFrames

[5]:

import geopandas
pth = libpysal.examples.get_path("mexicojoin.shp")
gdf = geopandas.read_file(pth)

from libpysal.weights import Queen, Rook, KNN

[6]:

%matplotlib inline
import matplotlib.pyplot as plt

[7]:

ax = gdf.plot()
ax.set_axis_off()
../../_images/user-guide_weights_weights_8_0.png

Contiguity Weights

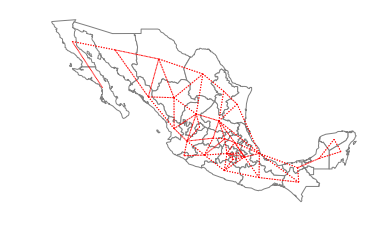
The first set of spatial weights we illustrate use notions of contiguity to define neighboring observations. Rook neighbors are those states that share an edge on their respective borders:

[8]:

w_rook = Rook.from_dataframe(gdf)

[9]:

w_rook.n

[9]:

32

[10]:

w_rook.pct_nonzero

[10]:

12.6953125

[11]:

ax = gdf.plot(edgecolor='grey', facecolor='w')
f,ax = w_rook.plot(gdf, ax=ax,
        edge_kws=dict(color='r', linestyle=':', linewidth=1),
        node_kws=dict(marker=''))
ax.set_axis_off()
../../_images/user-guide_weights_weights_13_0.png 
[12]:

gdf.head()

[12]:
POLY_ID AREA CODE NAME PERIMETER ACRES HECTARES PCGDP1940 PCGDP1950 PCGDP1960 ... GR9000 LPCGDP40 LPCGDP50 LPCGDP60 LPCGDP70 LPCGDP80 LPCGDP90 LPCGDP00 TEST geometry
0 1 7.252751e+10 MX02 Baja California Norte 2040312.385 1.792187e+07 7252751.376 22361.0 20977.0 17865.0 ... 0.05 4.35 4.32 4.25 4.40 4.47 4.43 4.48 1.0 (POLYGON ((-113.1397171020508 29.0177764892578...
1 2 7.225988e+10 MX03 Baja California Sur 2912880.772 1.785573e+07 7225987.769 9573.0 16013.0 16707.0 ... 0.00 3.98 4.20 4.22 4.39 4.46 4.41 4.42 2.0 (POLYGON ((-111.2061233520508 25.8027763366699...
2 3 2.731957e+10 MX18 Nayarit 1034770.341 6.750785e+06 2731956.859 4836.0 7515.0 7621.0 ... -0.05 3.68 3.88 3.88 4.04 4.13 4.11 4.06 3.0 (POLYGON ((-106.6210784912109 21.5653114318847...
3 4 7.961008e+10 MX14 Jalisco 2324727.436 1.967200e+07 7961008.285 5309.0 8232.0 9953.0 ... 0.03 3.73 3.92 4.00 4.21 4.32 4.30 4.33 4.0 POLYGON ((-101.52490234375 21.85663986206055, ...
4 5 5.467030e+09 MX01 Aguascalientes 313895.530 1.350927e+06 546702.985 10384.0 6234.0 8714.0 ... 0.13 4.02 3.79 3.94 4.21 4.32 4.32 4.44 5.0 POLYGON ((-101.8461990356445 22.01176071166992...

5 rows × 35 columns

[13]:

w_rook.neighbors[0] # the first location has two neighbors at locations 1 and 22

[13]:

[1, 22]

[14]:

gdf['NAME'][[0, 1,22]]

[14]:

0     Baja California Norte
1       Baja California Sur
22                   Sonora
Name: NAME, dtype: object

So, Baja California Norte has 2 rook neighbors: Baja California Sur and Sonora.

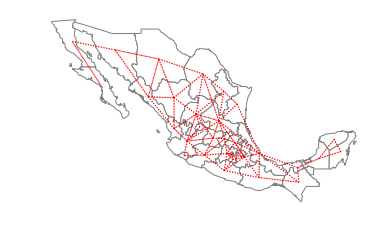
Queen neighbors are based on a more inclusive condition that requires only a shared vertex between two states:

[15]:

w_queen = Queen.from_dataframe(gdf)

[16]:

w_queen.n == w_rook.n

[16]:

True

[17]:

(w_queen.pct_nonzero > w_rook.pct_nonzero) == (w_queen.n == w_rook.n)

[17]:

True

[18]:

ax = gdf.plot(edgecolor='grey', facecolor='w')
f,ax = w_queen.plot(gdf, ax=ax,
        edge_kws=dict(color='r', linestyle=':', linewidth=1),
        node_kws=dict(marker=''))
ax.set_axis_off()
../../_images/user-guide_weights_weights_22_0.png 
[19]:

w_queen.histogram

[19]:

[(1, 1), (2, 6), (3, 6), (4, 6), (5, 5), (6, 2), (7, 3), (8, 2), (9, 1)]

[20]:

w_rook.histogram

[20]:

[(1, 1), (2, 6), (3, 7), (4, 7), (5, 3), (6, 4), (7, 3), (8, 1)]

[21]:

c9 = [idx for idx,c in w_queen.cardinalities.items() if c==9]

[22]:

gdf['NAME'][c9]

[22]:

28    San Luis Potosi
Name: NAME, dtype: object

[23]:

w_rook.neighbors[28]

[23]:

[5, 6, 7, 27, 29, 30, 31]

[24]:

w_queen.neighbors[28]

[24]:

[3, 5, 6, 7, 24, 27, 29, 30, 31]

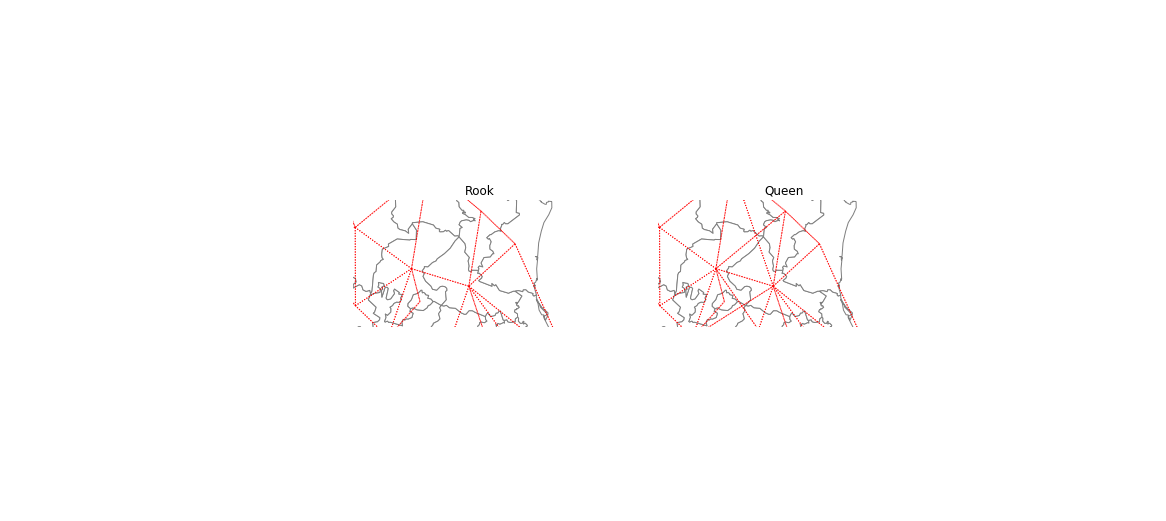
[25]:

import numpy as np
f,ax = plt.subplots(1,2,figsize=(10, 6), subplot_kw=dict(aspect='equal'))
gdf.plot(edgecolor='grey', facecolor='w', ax=ax[0])
w_rook.plot(gdf, ax=ax[0],
        edge_kws=dict(color='r', linestyle=':', linewidth=1),
        node_kws=dict(marker=''))
ax[0].set_title('Rook')
ax[0].axis(np.asarray([-105.0, -95.0, 21, 26]))

ax[0].axis('off')
gdf.plot(edgecolor='grey', facecolor='w', ax=ax[1])
w_queen.plot(gdf, ax=ax[1],
        edge_kws=dict(color='r', linestyle=':', linewidth=1),
        node_kws=dict(marker=''))
ax[1].set_title('Queen')
ax[1].axis('off')
ax[1].axis(np.asarray([-105.0, -95.0, 21, 26]))

[25]:

array([-105.,  -95.,   21.,   26.])
../../_images/user-guide_weights_weights_29_1.png 
[26]:

w_knn = KNN.from_dataframe(gdf, k=4)

[27]:

w_knn.histogram

[27]:

[(4, 32)]

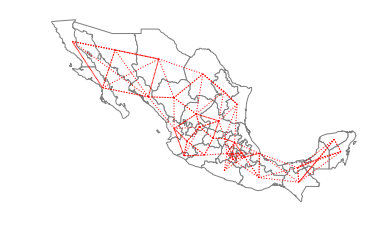
[28]:

ax = gdf.plot(edgecolor='grey', facecolor='w')
f,ax = w_knn.plot(gdf, ax=ax,
        edge_kws=dict(color='r', linestyle=':', linewidth=1),
        node_kws=dict(marker=''))
ax.set_axis_off()
../../_images/user-guide_weights_weights_32_0.png

Weights from shapefiles (without geopandas)

[29]:

pth = libpysal.examples.get_path("mexicojoin.shp")
from libpysal.weights import Queen, Rook, KNN

[30]:

w_queen = Queen.from_shapefile(pth)

[31]:

w_rook = Rook.from_shapefile(pth)

[32]:

w_knn1 = KNN.from_shapefile(pth)

/home/serge/Dropbox/p/pysal/src/subpackages/libpysal/libpysal/weights/weights.py:170: UserWarning: The weights matrix is not fully connected. There are 2 components
  warnings.warn("The weights matrix is not fully connected. There are %d components" % self.n_components)

The warning alerts us to the fact that using a first nearest neighbor criterion to define the neighbors results in a connectivity graph that has more than a single component. In this particular case there are 2 components which can be seen in the following plot:

[33]:

ax = gdf.plot(edgecolor='grey', facecolor='w')
f,ax = w_knn1.plot(gdf, ax=ax,
        edge_kws=dict(color='r', linestyle=':', linewidth=1),
        node_kws=dict(marker=''))
ax.set_axis_off()
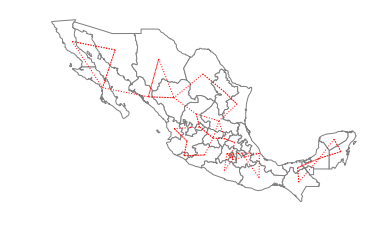
../../_images/user-guide_weights_weights_39_0.png

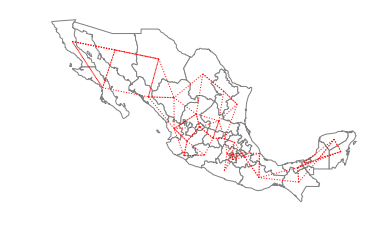
The two components are separated in the southern part of the country, with the smaller component to the east and the larger component running through the rest of the country to the west. For certain types of spatial analytical methods, it is necessary to have a adjacency structure that consists of a single component. To ensure this for the case of Mexican states, we can increase the number of nearest neighbors to three:

[34]:

w_knn3 = KNN.from_shapefile(pth,k=3)

[35]:

ax = gdf.plot(edgecolor='grey', facecolor='w')
f,ax = w_knn3.plot(gdf, ax=ax,
        edge_kws=dict(color='r', linestyle=':', linewidth=1),
        node_kws=dict(marker=''))
ax.set_axis_off()
../../_images/user-guide_weights_weights_42_0.png

Lattice Weights

[36]:

from libpysal.weights import lat2W

[37]:

w = lat2W(4,3)

[38]:

w.n

[38]:

12

[39]:

w.pct_nonzero

[39]:

23.61111111111111

[40]:

w.neighbors

[40]:

{0: [3, 1],
 3: [0, 6, 4],
 1: [0, 4, 2],
 4: [1, 3, 7, 5],
 2: [1, 5],
 5: [2, 4, 8],
 6: [3, 9, 7],
 7: [4, 6, 10, 8],
 8: [5, 7, 11],
 9: [6, 10],
 10: [7, 9, 11],
 11: [8, 10]}

Handling nonplanar geometries

[41]:

rs = libpysal.examples.get_path('map_RS_BR.shp')

[42]:

import geopandas as gpd

[43]:

rs_df = gpd.read_file(rs)
wq = libpysal.weights.Queen.from_dataframe(rs_df)

/home/serge/Dropbox/p/pysal/src/subpackages/libpysal/libpysal/weights/weights.py:168: UserWarning: There are 29 disconnected observations
  Island ids: 0, 4, 23, 27, 80, 94, 101, 107, 109, 119, 122, 139, 169, 175, 223, 239, 247, 253, 254, 255, 256, 261, 276, 291, 294, 303, 321, 357, 374
  " Island ids: %s" % ', '.join(str(island) for island in self.islands))

[44]:

len(wq.islands)

[44]:

29

[45]:

wq[0]

[45]:

{}

[46]:

wf = libpysal.weights.fuzzy_contiguity(rs_df)

[47]:

wf.islands

[47]:

[]

[48]:

wf[0]

[48]:

{239: 1.0, 59: 1.0, 152: 1.0, 23: 1.0, 107: 1.0}

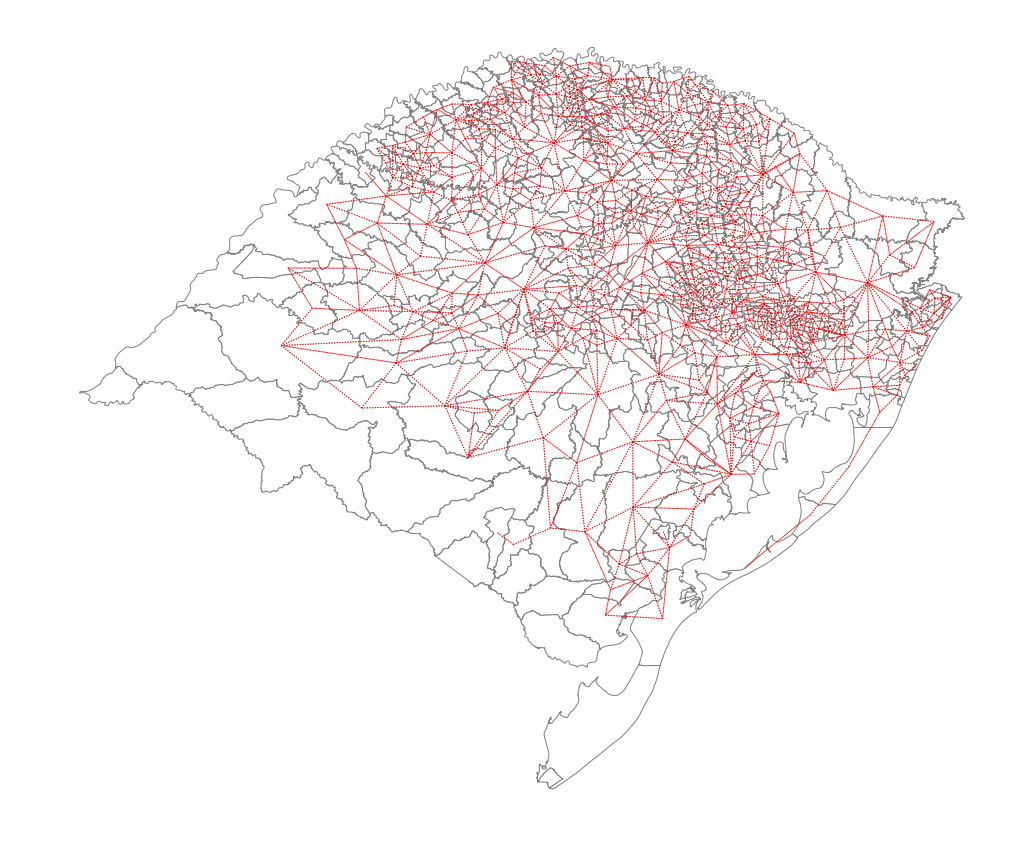
[49]:

plt.rcParams["figure.figsize"] = (20,15)
ax = rs_df.plot(edgecolor='grey', facecolor='w')
f,ax = wq.plot(rs_df, ax=ax,
        edge_kws=dict(color='r', linestyle=':', linewidth=1),
        node_kws=dict(marker=''))

ax.set_axis_off()
../../_images/user-guide_weights_weights_58_0.png 
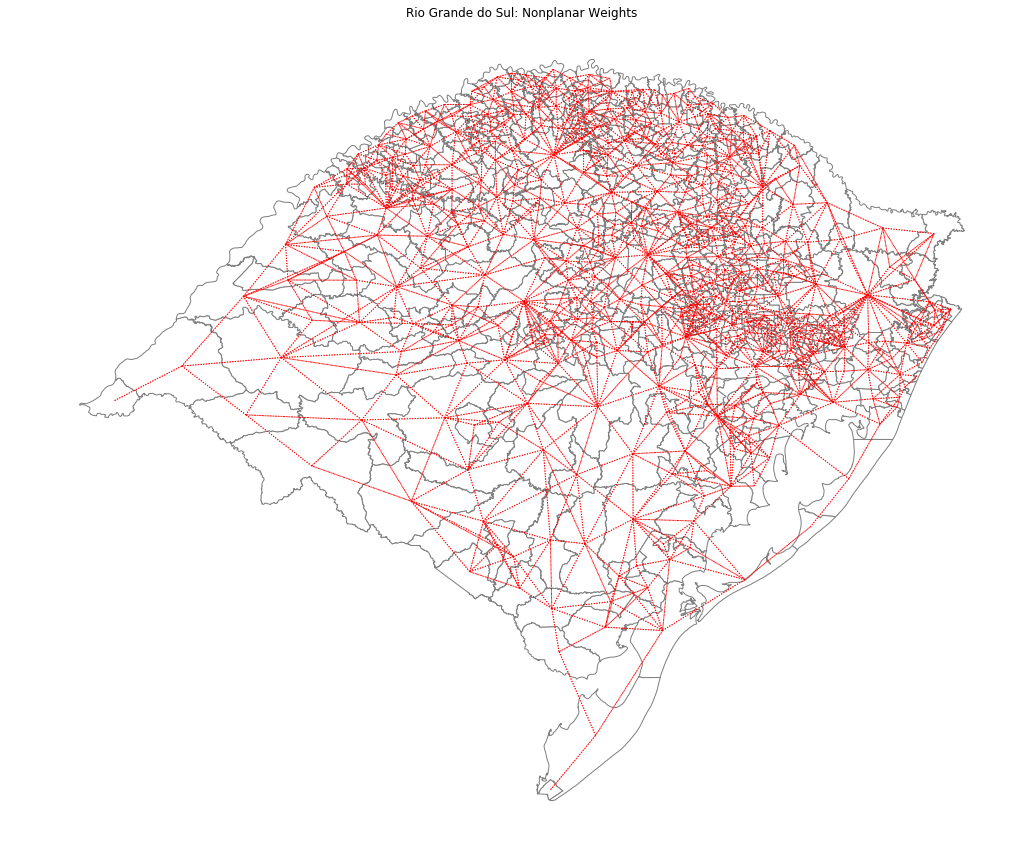
[53]:


ax = rs_df.plot(edgecolor='grey', facecolor='w')
f,ax = wf.plot(rs_df, ax=ax,
        edge_kws=dict(color='r', linestyle=':', linewidth=1),
        node_kws=dict(marker=''))
ax.set_title('Rio Grande do Sul: Nonplanar Weights')
ax.set_axis_off()
plt.savefig('rioGrandeDoSul.png')
../../_images/user-guide_weights_weights_59_0.png 
[ ]:



[ ]: