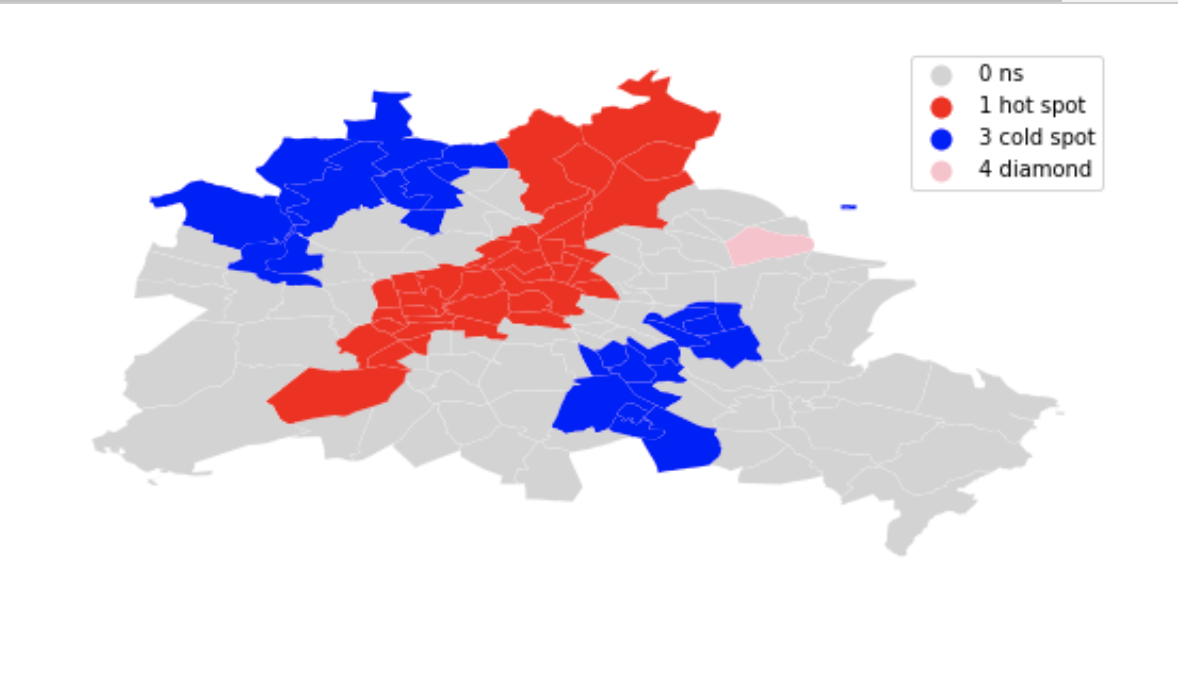
Esda implements methods for the analysis of both global (map-wide) and local (focal) spatial autocorrelation, for both continuous and binary data. In addition, the package increasingly offers cutting-edge statistics about boundary strength and measures of aggregation error in statistical analyses.
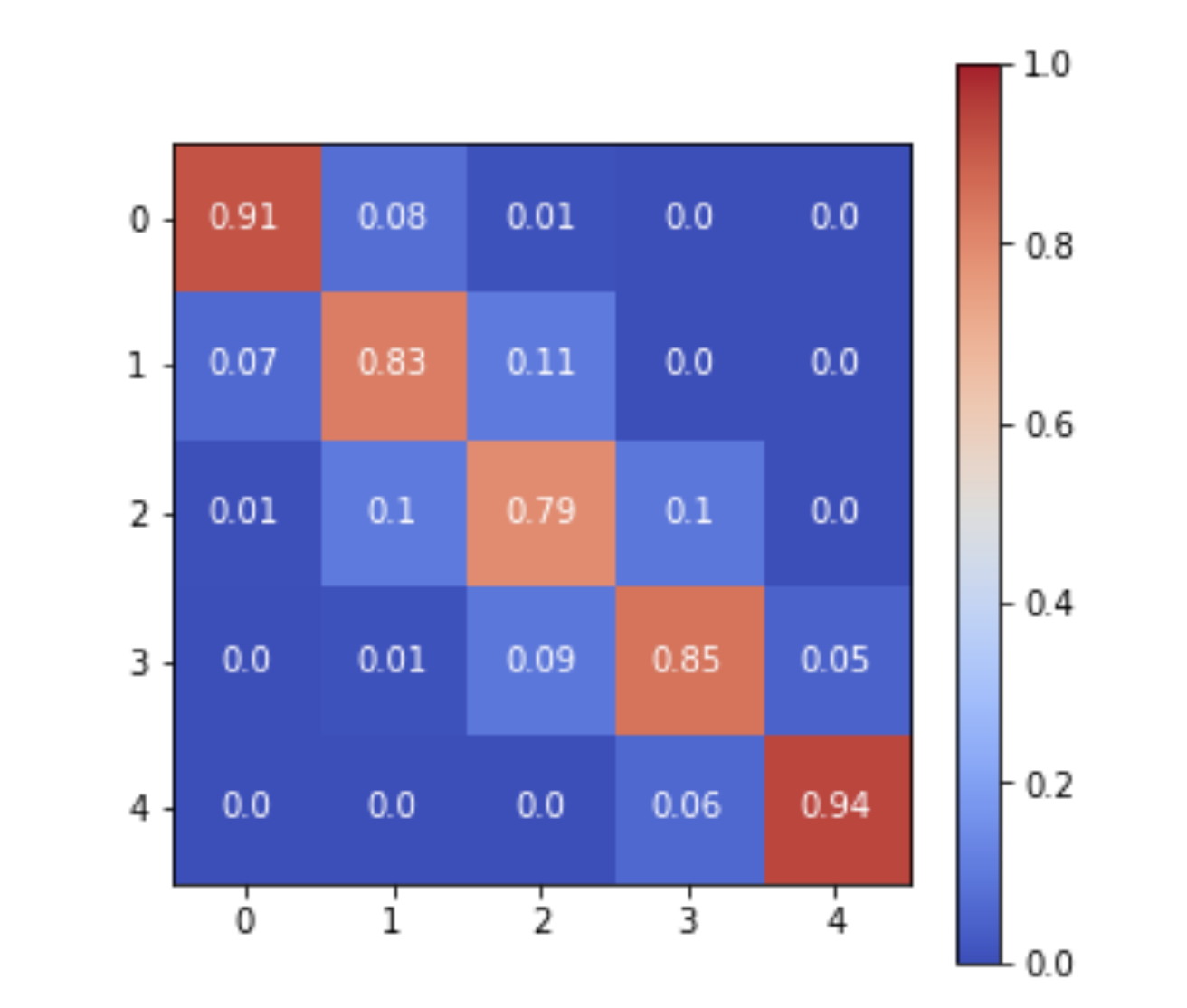
Giddy is an extension of Esda to spatio-temporal data. The package hosts state-of-the-art methods that explicitly consider the role of space in the dynamics of distributions over time.
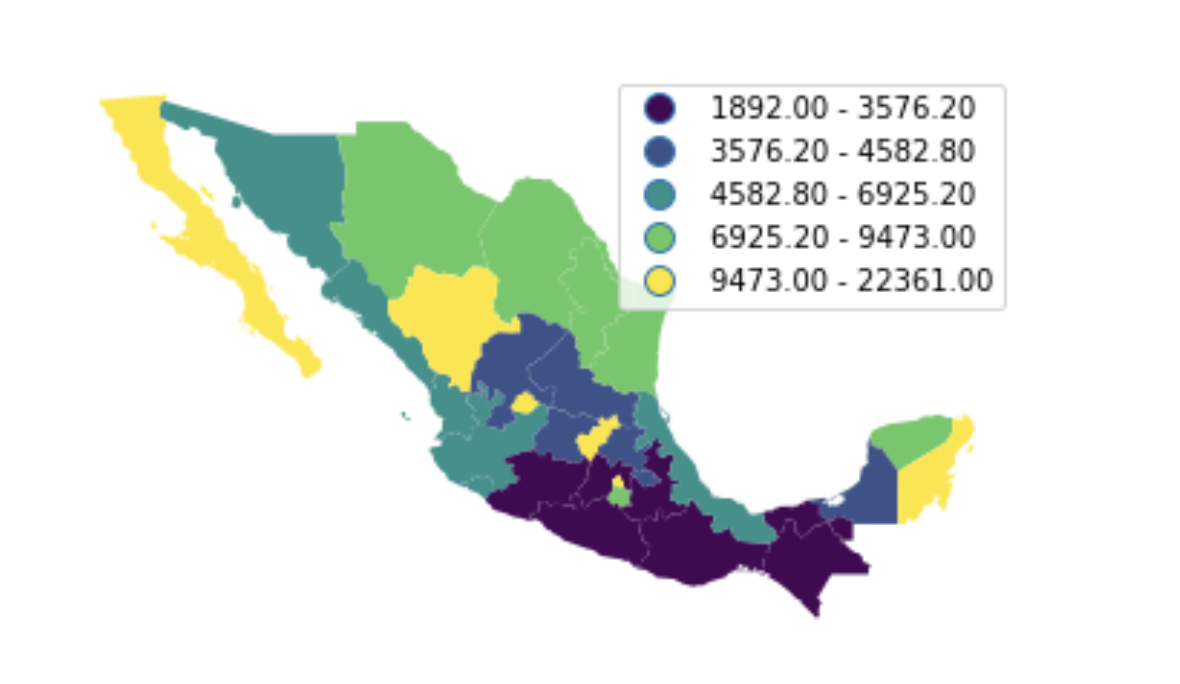
Inequality provides indices for measuring inequality over space and time. These comprise classic measures such as the Theil *T* information index and the Gini index in mean deviation form; but also spatially-explicit measures that incorporate the location and spatial configuration of observations in the calculation of inequality measures.
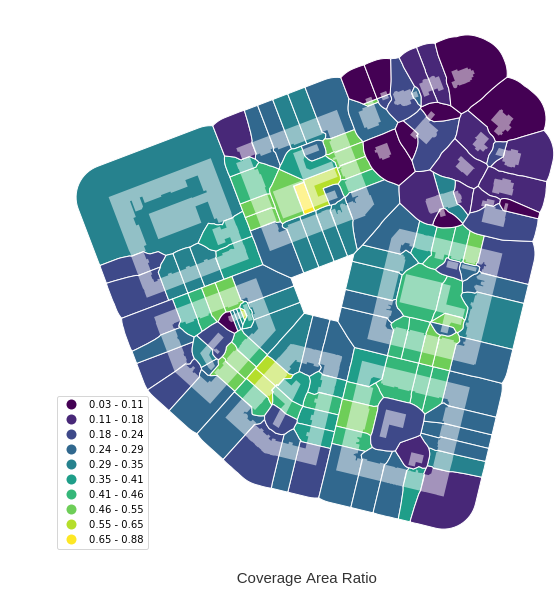
Momepy is a library for quantitative analysis of urban form - urban morphometrics. It aims to provide a wide range of tools for a systematic and exhaustive analysis of urban form. It can work with a wide range of elements, while focused on building footprints and street networks. momepy stands for Morphological Measuring in Python
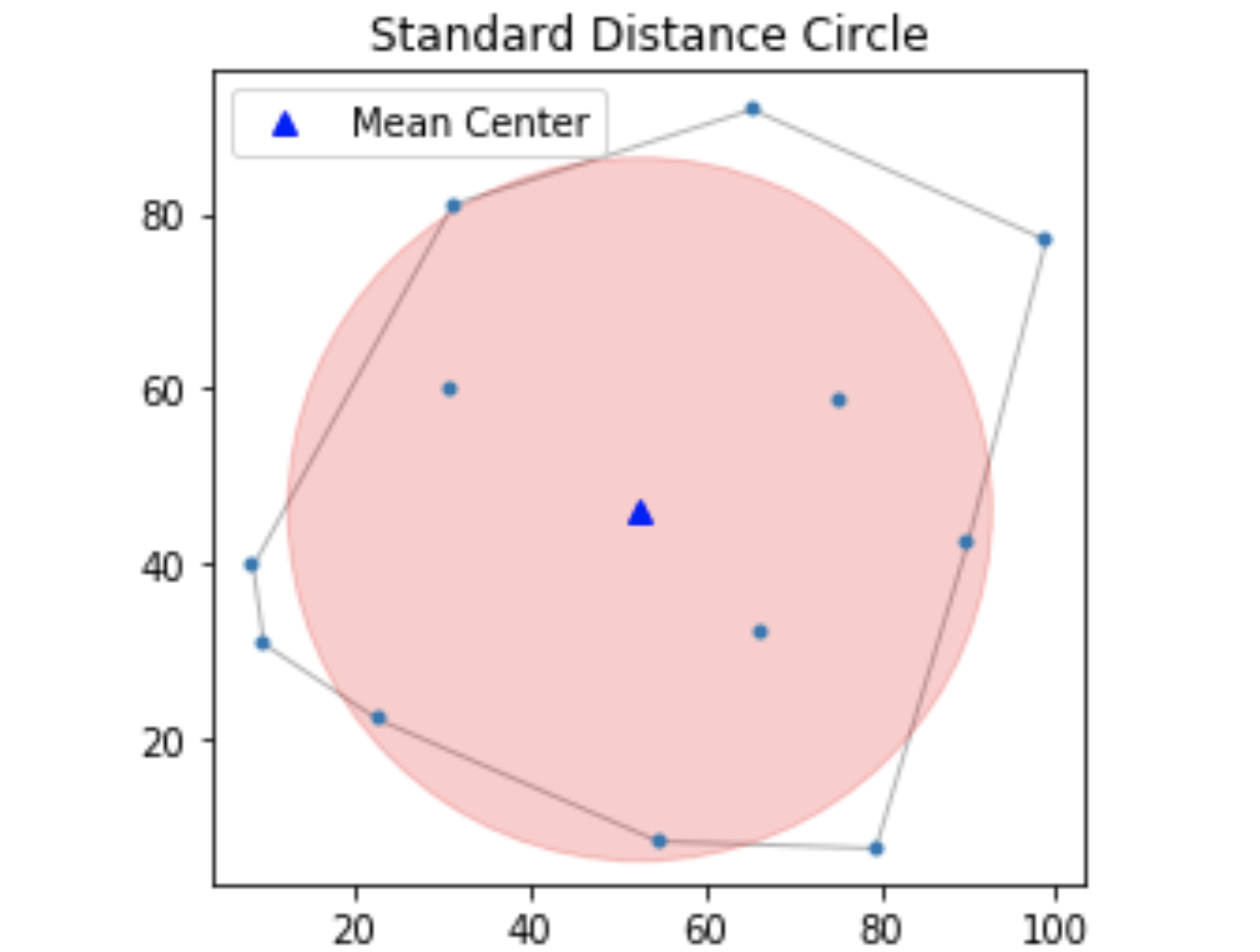
Pointpats supports the statistical analysis of point data, including methods to characterize the spatial structure of an observed point pattern: a collection of locations where some phenomena of interest have been recorded. This includes measures of centrography which provide overall geometric summaries of the point pattern, including central tendency, dispersion, intensity, and extent.
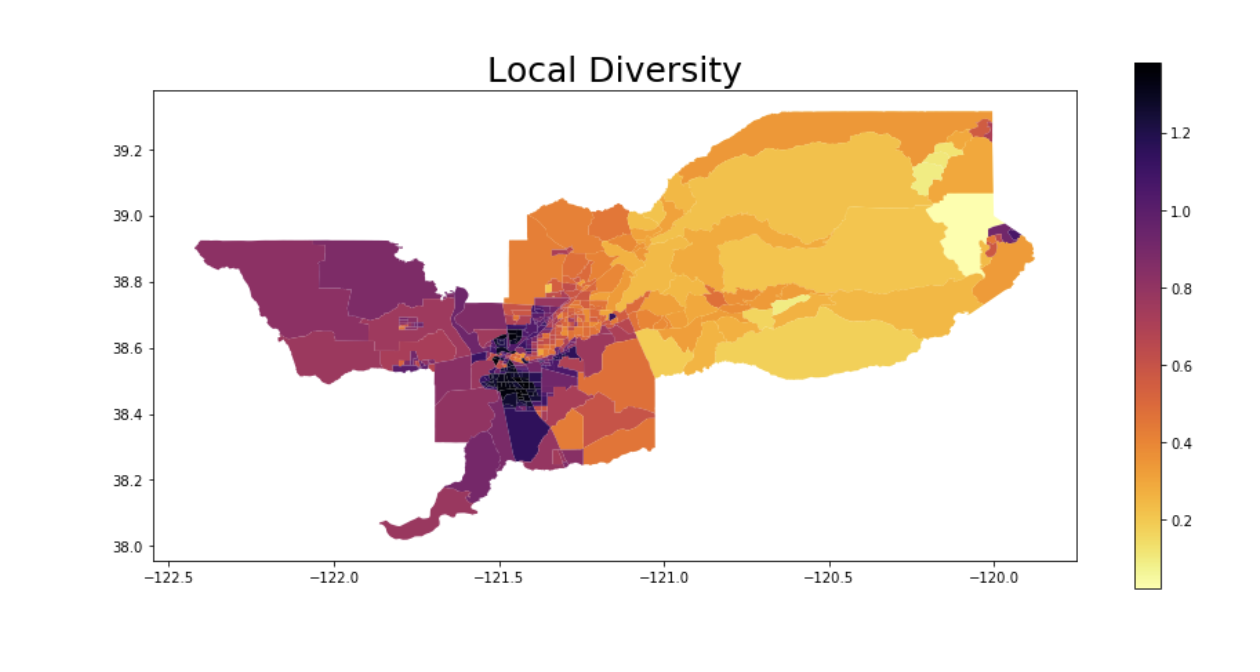
The Segregation package calculates over 40 different segregation indices and provides a suite of additional features for measurement, visualization, and hypothesis testing that together represent the state-of-the-art in quantitative segregation analysis.
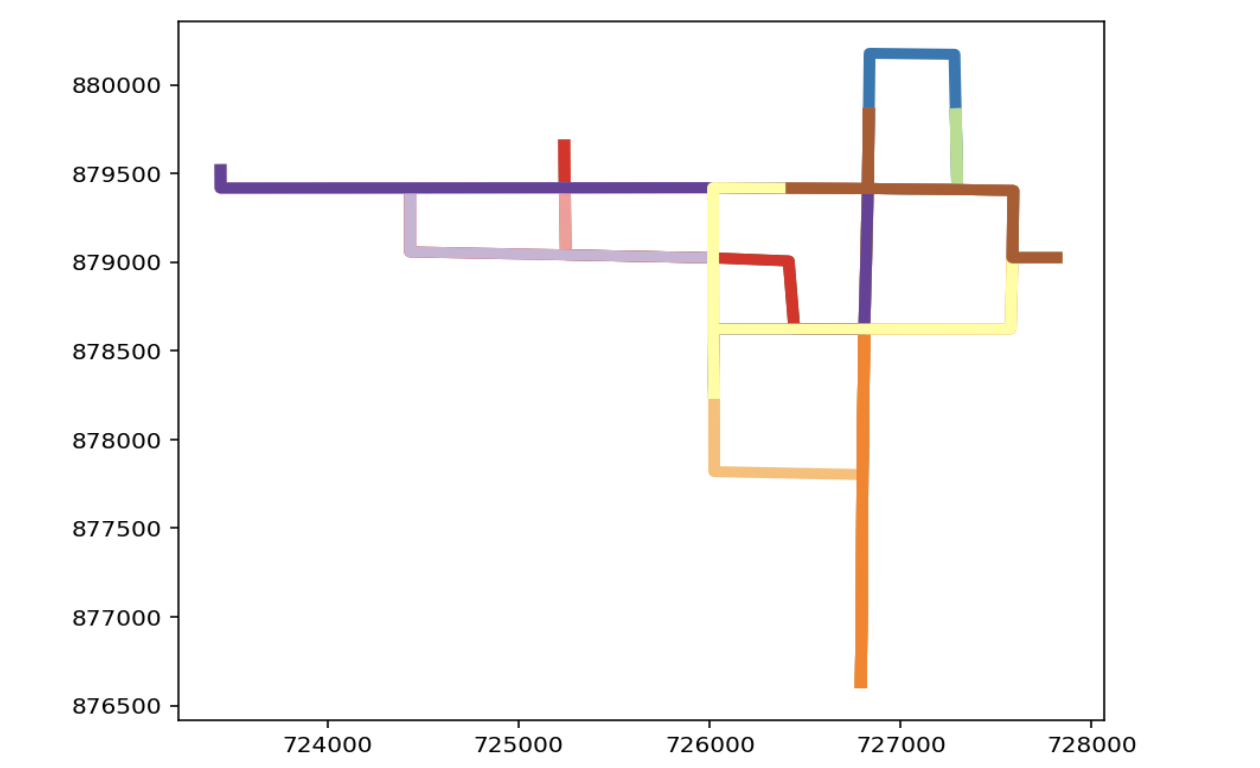
Spaghetti supports the spatial analysis of graphs, networks, topology, and inference. It includes a robust all-to-all Dijkstra shortest path algorithm, the ability to connect near-network observations onto the network, functionality for the statistical testing of clusters on networks, and high-performance geometric and spatial computations.