sparse_grav
import numpy as np
import pandas as pd
from gravity import Gravity, Production, Attraction, Doubly, BaseGravity
from entropy import Unconstrained, ProductionConstrained, AttractionConstrained, DoublyConstrained
import statsmodels.formula.api as smf
from statsmodels.api import families
import matplotlib.pyplot as plt
%pylab inline
import time
def timeit(method):
def timed(*args, **kw):
ts = time.time()
result = method(*args, **kw)
te = time.time()
elapsed = te-ts
#print '%2.8f sec' % \
#(elapsed)
return result, elapsed
return timed
@timeit
def gravity(f ,o, d, o_vars, d_vars, dij, cost='exp', framework='glm'):
results = Gravity(f, o_vars, d_vars, dij, cost, framework=framework)
return results
@timeit
def production(f ,o, d, o_vars, d_vars, dij, cost='exp', framework='glm'):
results = Production(f, o, d_vars, dij, 'exp', framework=framework)
return results
@timeit
def attraction(f ,o, d, o_vars, d_vars, dij, cost='exp', framework='glm'):
results = Attraction(f, d, o_vars, dij, 'exp', framework=framework)
return results
@timeit
def doubly(f ,o, d, o_vars, d_vars, dij, cost='exp', framework='glm'):
results = Doubly(f, o, d, dij, 'exp', framework=framework)
return results
def sim_data(n):
o = np.tile(np.arange(n),n)
d = np.repeat(np.arange(n),n)
loc_size = np.random.randint(25000,500000, n)
o_vars = np.tile(loc_size, n)
d_vars = np.repeat(loc_size, n)
dij = np.random.exponential(2500, n**2)
f = o_vars**.3*d_vars**.4*np.exp(dij*-.00005)
o = np.reshape(o, (-1,1))
d = np.reshape(d, (-1,1))
o_vars = np.reshape(o_vars, (-1,1))
d_vars = np.reshape(d_vars, (-1,1))
dij = np.reshape(dij, (-1,1))
f = np.reshape(f, (-1,1))
f = f.astype(np.int64)
return f, o, d, o_vars, d_vars, dij
def loop(func, start, stop, step, framework='glm'):
results = []
for n in np.arange(start, stop, step):
f, o, d, o_vars, d_vars, dij = sim_data(n)
out, elapsed = func(f, o, d, o_vars, d_vars, dij, 'exp', framework=framework)
print out.params[-2:]
results.append(elapsed)
return results
grav = loop(gravity, 25, 500, 25)
prod = loop(production, 25, 500, 25)
att = loop(attraction, 25, 500, 25)
doub = loop(doubly, 25, 500, 25)
grav
prod
att
doub
x = np.arange(25, 500, 25)
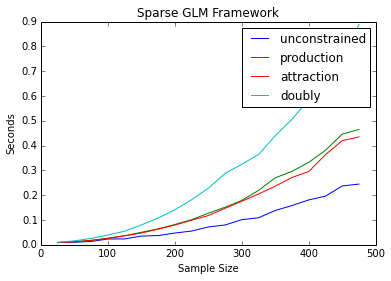
plt.plot(x, grav, x, prod, x, att, x, doub)
plt.legend(('unconstrained', 'production', 'attraction', 'doubly'))
plt.title('Sparse GLM Framework')
plt.xlabel('Sample Size')
plt.ylabel('Seconds')